فهرست مطالب
-
اتصال سری و موازی مقاومت ها
-
خلاصه
مقاومتها را میتوان در ترکیبهای نامحدود سری و موازی به یکدیگر متصل کرد و مدارهای مقاومتی پیچیدهای را تشکیل داد.
در آموزشهای قبلی یاد گرفتیم که چگونه با اتصال مقاومتها به یکدیگر، یک شبکه مقاومت سری یا موازی تشکیل دهیم و از قانون اهم برای یافتن جریانها و ولتاژهای مختلف در هر ترکیب استفاده کردیم.
اما اگر بخواهیم مقاومتهای مختلف را در «هر دو» ترکیب موازی و سری در همان مدار، برای تولید شبکههای مقاومت پیچیدهتر، به طور هم زمان متصل کنیم چطور؟ چگونه میتوان مقاومت کل مدار، جریانها و ولتاژهای این ترکیبهای مقاومتی را محاسبه کرد؟
مدارهای مقاومتی که شبکههای مقاومت سری و موازی را با هم ترکیب میکنند، به طور کلی به عنوان ترکیب مقاومتی یا مدار مقاومت ترکیبی شناخته میشوند. روش محاسبه مقاومت معادل در این مدارها همان روشی است که برای هر مدار جداگانه سری یا موازی وجود دارد و امیدواریم اکنون بدانید که مقاومتهای سری دقیقا جریان یکسانی دارند و ولتاژ دو سر مقاومتهای موازی نیز ولتاژ یکسانی است.
مثال ۱
به عنوان مثال، در مدار شکل زیر جریان کل (IT) گرفته شده از منبع ۱۲ ولت را محاسبه کنید.
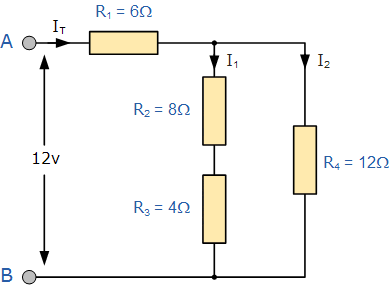
در نگاه اول، این کار دشوار به نظر میرسد، اما اگر کمی دقیقتر نگاه کنیم، میبینیم که دو مقاومت R۲ و R۳ در واقع به صورت «سری» به هم متصل شدهاند؛ بنابراین میتوانیم آنها را با هم جمع کنیم تا یک مقاومت معادل ایجاد کنیم. همان کاری که در آموزش مقاومتهای سری انجام دادیم. مقاومت حاصل از این ترکیب بدین ترتیب خواهد بود:
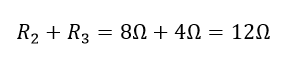
بنابراین میتوانیم مقاومتهای R۲ و R۳ را با یک مقاومت واحد با مقدار ۱۲Ω جایگزین کنیم.
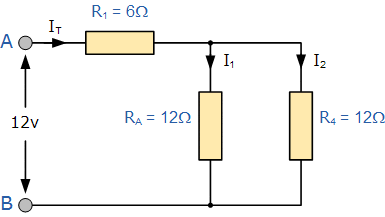
حال مدار ما یک مقاومت واحد (RA) دارد که با مقاومت R۴ موازی است. با استفاده از معادله مقاومتهای موازی میتوانیم این ترکیب را به یک مقاومت معادل واحد با مقدار R(combination) به شرح زیر کاهش دهیم.
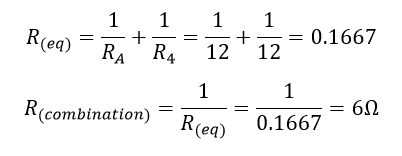
اکنون مدار مقاومتی حاصل شبیه به شکل زیر است:
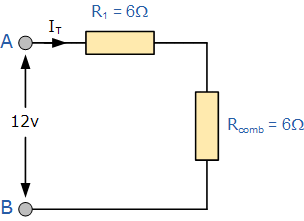
میتوانیم ببینیم که دو مقاومت باقی مانده، R۱ و R(comb)،در یک ترکیب «سری» به هم متصل شدهاند و مانند قبل (اتصال سری مقاومتها) میتوان مقادیر آنها را با هم جمع کرد. در نتیجه، مقاومت کل مدار بین نقاط A و B به شرح زیر به دست میآید:
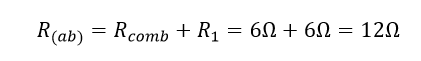
بنابراین میتوان چهار مقاومت اصلی را که در مدار اولیه به هم متصل شدهاند، تنها با یک مقاومت ۱۲Ω جایگزین کرد.
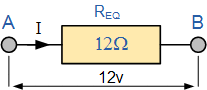
با استفاده از قانون اهم، مقدار جریان (I) عبوری از مدار به شکل زیر محاسبه میشود:
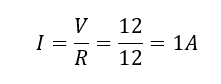
پس میتوانیم ببینیم که با استفاده از مراحل بالا و جایگزین کردن همه مقاومتهای متصل به هم (به طور سری یا موازی)، میتوان هر مدار مقاومتی پیچیده متشکل از چندین مقاومت را به یک مدار ساده و تنها با یک مقاومت معادل کاهش داد.
ما میتوانیم یک مرحله جلوتر رفته و با استفاده از قانون اهم جریانهای دو شاخه، I۱ و I۲ را به صورت زیر به دست آوریم.
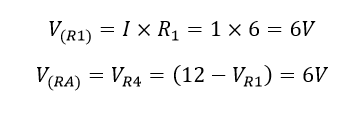
بنابراین:
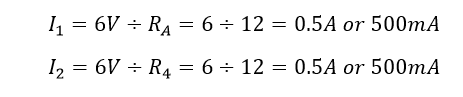
از آنجا که مقادیر مقاومت دو شاخه یکسان و برابر با 12Ω است، جریانهای I۱ و I۲ نیز هر یک برابر 0.5A (یا 500mA) هستند. بنابراین جریان کل IT که منبع تغذیه فراهم میکند، همان طور که در بالا محاسبه شده، برابر است با
0.5 + 0.5 = 1A.
در تركیبها یا شبکههای مقاومتی پیچیده، گاهی بهتر است که پس از محاسبات و اعمال تغییرات، مدار جدید را دوباره رسم کنید، زیرا این کمک تصویری محاسبات شما را آسانتر میكند. سپس به جایگزین کردن ترکیبهای سری و موازی ادامه دهید تا یک مقاومت معادل (REQ) به دست آید. بیایید یک مدار ترکیب مقاومتی پیچیدهتر را امتحان کنیم.
مثال ۲
مقاومت معادل REQ را برای ترکیب مقاومتی زیر به دست آورید.
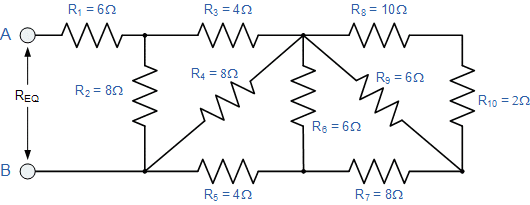
بار دیگر، ممکن است در نگاه اول این شبکه نردبانی مقاومت پیچیده به نظر برسد، اما مانند قبل، تنها ترکیبی از مقاومتهای سری و موازی متصل به هم است. با شروع از سمت راست و استفاده از معادله ساده شده برای دو مقاومت موازی، میتوانیم مقاومت معادل ترکیب R۸، R۹ و R۱۰ را پیدا کنیم و آن را RA بنامیم.
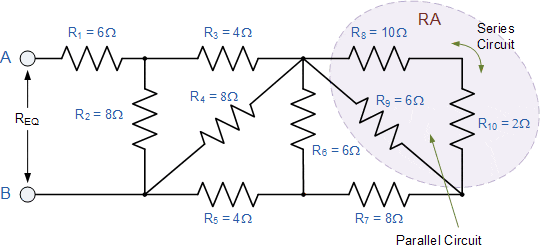
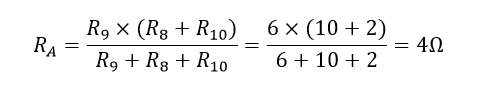
همانطور که در شکل نشان داده شده، RA و R۷ سری هستند، بنابراین مقاومت معادل آنها RA + R۷ = ۴ + ۸ = ۱۲Ω خواهد بود.
این مقدار مقاومت 12Ω اکنون با R۶ موازی است و می تواند با نام RB محاسبه شود.
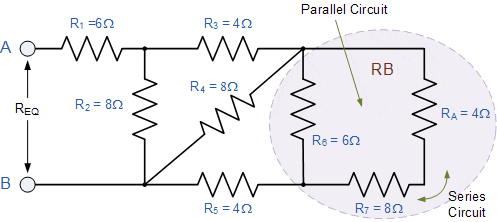
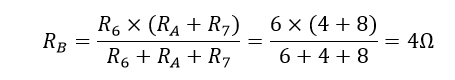
همانطور که در شکل نشان داده شده، RB و R۵ سری هستند، بنابراین مقاومت معادل آنها RB + R۵ = ۴ + ۴ = ۸Ω خواهد بود.
این مقدار مقاومت 8Ω اکنون با R۴ موازی است و می تواند با نام RC محاسبه شود.
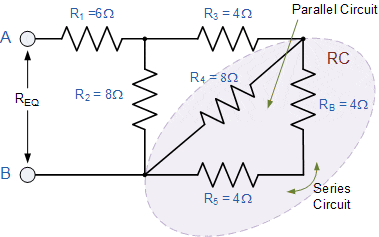
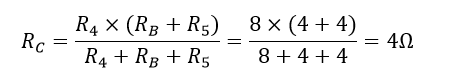
همانطور که در شکل نشان داده شده، RC و R۳ سری هستند، بنابراین مقاومت معادل آنها RC + R۳ = ۸Ω خواهد بود.
این مقدار مقاومت 8Ω اکنون با R۲ موازی است و می تواند با نام RD محاسبه شود.
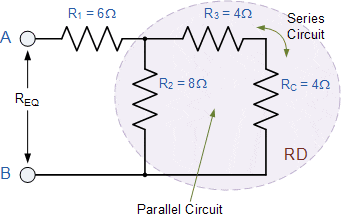
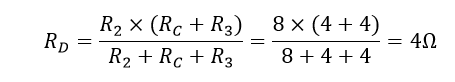
همانطور که در شکل نشان داده شده، RD و R۱ سری هستند، بنابراین مقاومت معادل آنها RD + R۱ = ۴ + ۶ = ۱۰Ω خواهد بود.
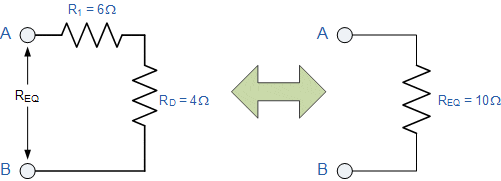
پس شبکه مقاومتی پیچیده بالا متشکل از ده مقاومت سری و موازی متصل به هم، میتواند تنها با یک مقاومت معادل (REQ) به ارزش ۱۰Ω جایگزین شود.
خلاصه
هنگام حل هر مدار مقاومت ترکیبی که از شاخههای موازی و سری تشکیل شده است، اولین قدمی که باید برداریم شناسایی شاخههای سری و موازی ساده و جایگزین کردن آنها با مقاومتهای معادل است.
این مرحله به ما امکان میدهد تا پیچیدگی مدار را کاهش دهیم و کمک میکند تا یک مدار مقاومت ترکیبی پیچیده را به یک مقاومت معادل واحد تبدیل کنیم. به یاد داشته باشید که مدارهای سری تقسیم کننده ولتاژ و مدارهای موازی تقسیم کننده جریان هستند.
با این حال، محاسبات شبکههای پیچیدهتر مانند تضعیف کننده T-pad و پل مقاومتی، که نمیتوان آنها را با استفاده از مقاومتهای معادل به یک مدار موازی یا سری ساده کاهش داد، به روش دیگری نیاز دارند. این مدارهای پیچیدهتر باید با استفاده از قوانین جریان و ولتاژ کیرشهف حل شوند که در آموزش دیگری به آنها پرداخته خواهد شد.
در مقاله بعدی در مورد مقاومتها، به اختلاف پتانسیل الکتریکی (ولتاژ) بین دو نقطه، از جمله مقاومت، خواهیم پرداخت.
منبع:ردرونیک