فهرست مطالب
-
جمع حاصل ضرب
-
گیت AND (ضرب)
-
ترم ضرب (AND)
-
عبارتهای ضرب جبر بولی
-
ترم جمع (OR)
-
گیت OR (جمع)
-
جمع حاصلضربها
-
عبارت جمع حاصلضرب
-
تبدیل یک عبارت SOP به یک جدول درستی
-
جدول درستی جمع حاصلضرب
گیت AND (ضرب)
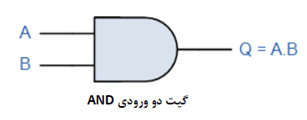
برخلاف ریاضیات مرسوم که از علامت ضربدر (x) یا ستاره (*) برای نمایش عمل ضرب، استفاده میشود؛ تابع AND در ضرب بولی با یک تک “نقطه” (.) نشان داده میشود. بنابراین، معادلهی بولی برای گیت AND با دو ورودی بهصورت: Q=A.B است و Q برابر با A AND B میباشد. برای یک ترم حاصلضرب، این متغیرهای ورودی، میتواند “صحیح (true)” یا “غلط (false)”، “1” یا “0” یا مکمل آنها باشند. بنابراین ترمهای زیر همگی ترمهای طبقهبندیشده بهعنوان ترمهای حاصلضرب هستند.
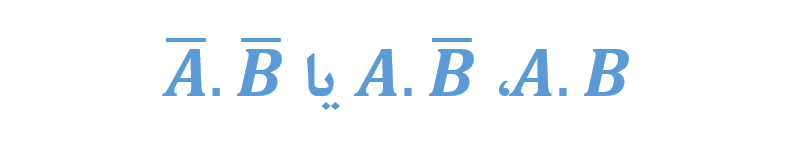
ترم ضرب (AND)
پس الان میدانیم؛ که در جبر بولی، “حاصلضرب” بهمعنای AND نمودن عبارتها با متغیرهای عبارت حاصلضرب است؛ که یک مثال شکل واقعی یا مکمل دارد؛ بهطوریکه حاصلضرب را نمیتوان بیشتر ساده کرد. این ترمها بهعنوان ترم میانی (midterms) نیز شناخته میشوند. حال چگونه میتوانیم عملکرد این تابع “حاصلضرب” را در جبر بولی، نشان دهیم؟!
یک عبارت حاصلضرب میتواند یک یا دو متغیر مستقل مانند A و B یا یک یا دو ثابت 0 و 1 داشته باشد. میتوانیم از این متغیرها و ثابتها در انواع ترکیبهای مختلف استفاده کنیم و نتیجهی ضرب را همانطور که در لیستهای زیر آمده است؛ نشان دهیم.
عبارتهای ضرب جبر بولی
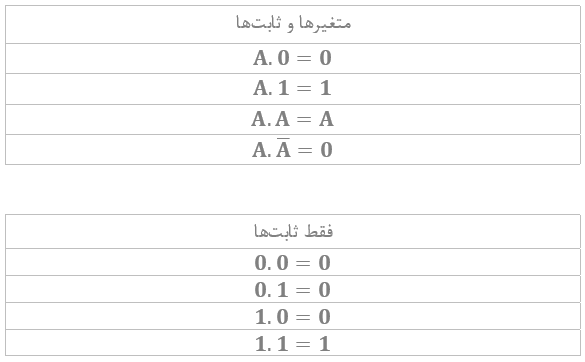
توجه داشته باشید؛ که “متغیر” بولی، میتواند یکی از دو مقدار “1” یا “0” را داشته باشد و مقدار خود را تغییر دهد. برای مثال، A=0 یا A=1. درحالیکه، یک “ثابت” بولی میتواند یکی از دو شکل “1” یا “0” را داشته باشد که مقدار ثابت است و بنابراین، نمیتواند تغییر کند.
پس هر حاصلضرب بولی دادهشده را میتوان به یک ثابت یا متغیر تنها، سادهسازی کرد. توضیح مختصری از قوانین بولی مختلف در ادامه آمده است؛ که در آن “A” یک ورودی متغیر را نشان میدهد.
قانون تطابق (Identity Law): یک عبارت AND شده با 1 ، همیشه برابر با خود عبارت است(A.1=A)
قانون خنثیکردن (Annulment Law) : یک عبارت AND شده با 0 ، همیشه برابر با 0 است(A.0=0)
قانون همانی (Idempotent Law): یک عبارت AND شده با خودش ، همیشه برابر با خود عبارت است(A.A=A)
قانون متمم (Complement Law): یک عبارت AND شده با مکمل خود ، همیشه برابر با 0 است(A.Ā =0)
قانون جابجایی (Commutative Law): ترتیب در دو عبارت که باهم AND شدهاند، یکسان است.(A.1=1.A)
ترم جمع (OR)
درحالیکه، تابع AND، معمولا بهعنوان عبارت حاصلضرب است؛ تابع OR بهعنوان ترم جمع شناخته میشود. تابع OR، معادل ریاضیاتی جمع است؛ که با نماد بهعلاوه (+) بیان میشود. از اینرو، گیت OR با دو ورودی، دارای ترم خروجی است؛ که بیان بولی آن، A+B است؛ زیرا مجموع منطقی A و B میباشد.
گیت OR (جمع)
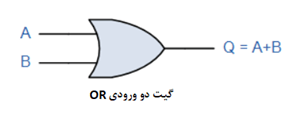
این جمع منطقی، معمولا بهعنوان جمع بولی شناخته میشود؛ زیرا یک تابع OR، جمع ترم دو یا چند متغیر یا ثابت ورودی است. در آموزش بعدی، نگاهی با جزئیات بیشتر به تابع OR و جمع بولی آن خواهیم داشت؛ اما اکنون، باید بخاطر بسپاریم؛ که تابع OR، نشاندهندهی عبارت جمع است.
جمع حاصلضربها
تا اینجا مشاهده کردیم؛ که تابع AND، حاصلضرب منطقی ضرب بولی و تابع OR، مجموع منطقی جمع بولی را تولید میکند. اما هنگام سروکار داشتن با مدارهای منطقی ترکیبی که در آنها، گیتهای AND، گیتهای OR و گیتهای NOT بههم متصل شدهاند؛ عبارتهای جمع حاصلضربها یا حاصلضرب جمعها، بهصورت گستردهای کاربرد دارد.
جمع حاصلضرب از این واقعیت ناشی میشود؛ که دو یا چند حاصلضرب (AND) با یکدیگر جمع (OR) شدهاند. به این معنا، که خروجیهای دو یا چند گیت AND به ورودی گیت OR متصل میشوند تا بهطور موثری باهم OR شوند و خروجی منطقی AND-OR نهایی را ایجاد نمایند. برای مثال، تابع بولی زیر، یک عبارت جمع حاصلضرب معمولی است:
عبارت جمع حاصلضرب
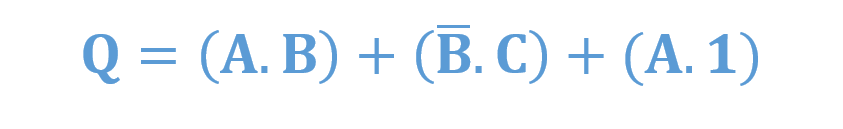
و نیز،
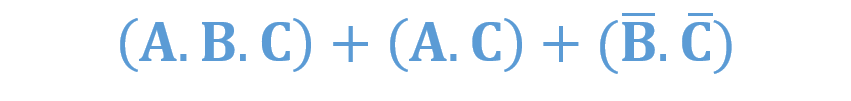
با اینحال، توابع بولی میتوانند بهصورت اشکال غیراستاندارد جمع حاصلضربها، همانند آنچه در زیر آمده است؛ نشان داده شوند؛ اما میتوان با گسترش عبارت، آن را به فرم SOP استاندارد، تبدیل کرد.
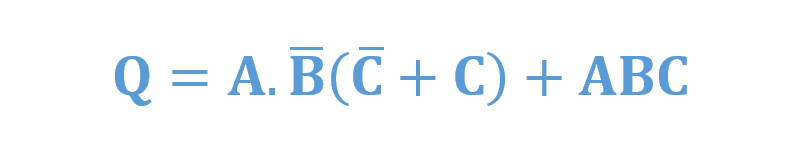
ترمهای جمع حاصلضرب بهصورت زیر در میآیند:
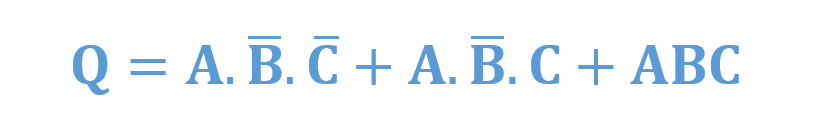
در واقع، این عبارت SOP بزرگ، میتواند با استفاده از قوانین جبر بولی، بیشتر کاهش یابد تا عبارت کاهشیافتهی SOP را تولید کند:
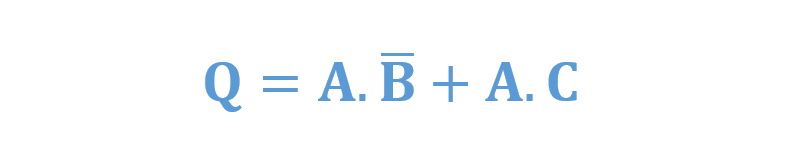
تبدیل یک عبارت SOP به یک جدول درستی
ما میتوانیم هر عبارت جمع-حاصلضرب را به شکل جدول درستی نمایش دهیم؛ زیرا هر ترکیب ورودی که خروجی منطقی “1” را تولید کند،؛ یک ترم حاصلضرب یا AND است؛ همانطور که در شکل زیر آمده است.
عبارت جمع حاصلضرب زیرا را در نظر بگیرید:
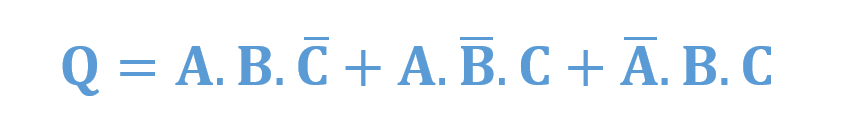
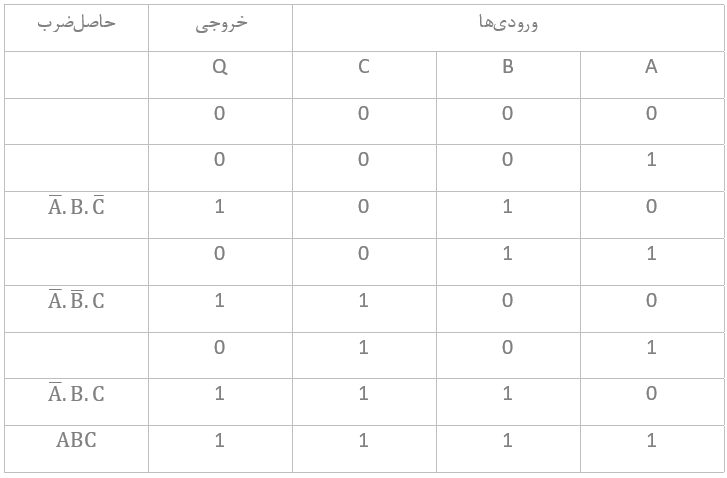
اکنون میتوانیم، جدول درستی را برای عبارت بالا، ترسیم کنیم، تا فهرستی از تمام ترکیبهای ورودی ممکت برای A، B و C نشان داده شود؛ که منجر به خروجی “1” میشود.
جدول درستی جمع حاصلضرب
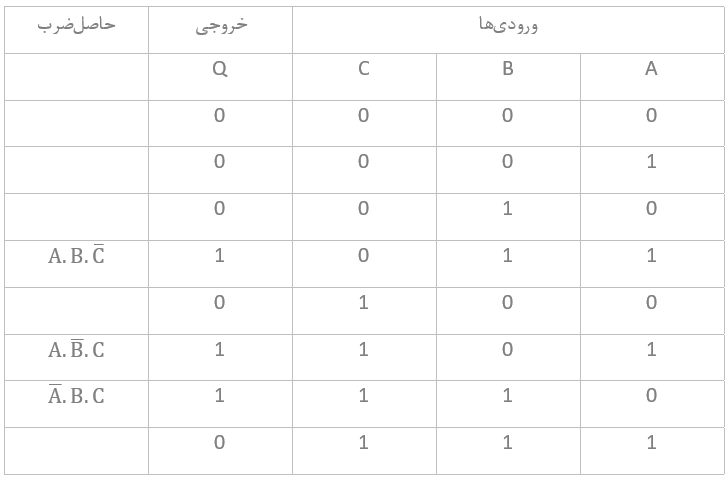
پس میتوانیم بهوضوح از جدول درستی ببینیم؛ که هر سطح حاصلضرب که یک “1” را برای خروجی تولید میکند؛ با عبارت ضرب بولی، مطابقت دارد و همهی سطحهای دیگری که خروجی “0” دارند؛ بهدلیل خارج شدن یک “1” از گیت OR است.
مثال جمع حاصلضرب
عبارت جبر بولی زیر، به این صورت داده شدهاست:
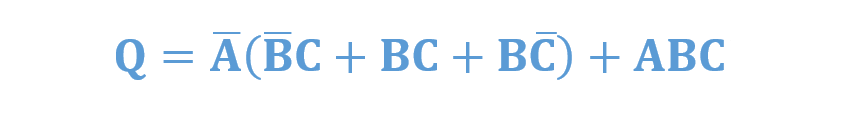
- معادلهی منطقی را به یک عبارت SOP معادل، تبدیل کنید.
- با استفاده از جدول درستی، تمام ترکیببندیهای ممکن را برای شرایط ورودی، که سبب تولید خروجی میشوند؛ نشان دهید.
- یک دیاگرام گیت منطقی برای این عبارت، رسم کنید.
- تبدیل به ترم SOP
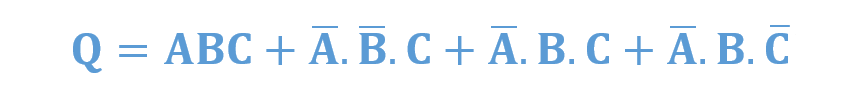
- جدول درستی
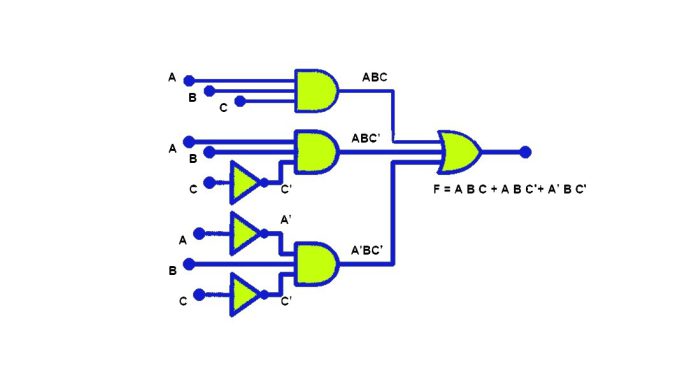
- دیاگرام گیت منطقی SOP
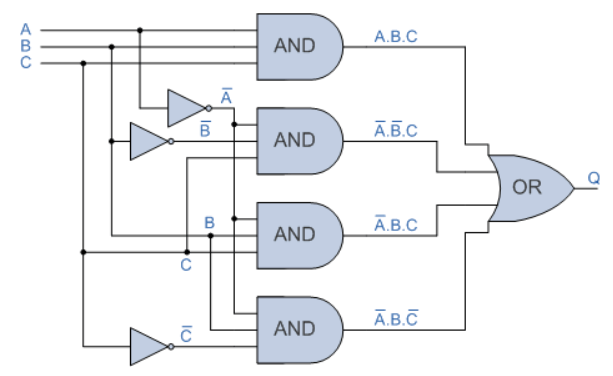
پس در این آموزش دیدیم؛ که عبارت جمع- حاصلضربها (SOP)، یک عبارت بولی استاندارد است؛ که دو یا چند “حاصلضرب” را باهم “جمع میکند” و برای یک مدار منطقی دیجیتال، عبارت SOP به این صورت است؛ که خروجی، شامل دو یا چند گیت منطقی AND است، که باهم OR شدهاند؛ تا خروجی نهایی (AND-OR) را بسازند.
منبع
منبع : ردرونیک