مقدمه منطق فازی
مفاهیم نادقیق بسیاری در پیرامون ما وجود دارند که آنها را به صورت روزمره در قالب عبارتهای مختلف بیان میکنیم. به این جمله دقت کنید: ” هوا خوب است.” هیچ کمیتی برای خوب بودن هوا مطرح نیست تا آن را اندازه بگیریم بلکه این یک حس کیفی است. در واقع مغز انسان با در نظر گرفتن فاکتورهای مختلف و براساس تفکر استنتاجی جملات را تعریف و ارزش گذاری مینماید که مدل سازی آنها به زبان و فرمولهای ریاضی اگر غیر ممکن نباشد کاری بسیار پیچیده خواهد بود.
منطق فازی تکنولوژی جدیدی است که شیوههایی را که برای طراحی و مدل سازی یک سیستم نیازمند ریاضیات پیچیده و پیشرفته است، با استفاده از مقادیر زبانی و دانش فرد خبره جایگزین میسازد.
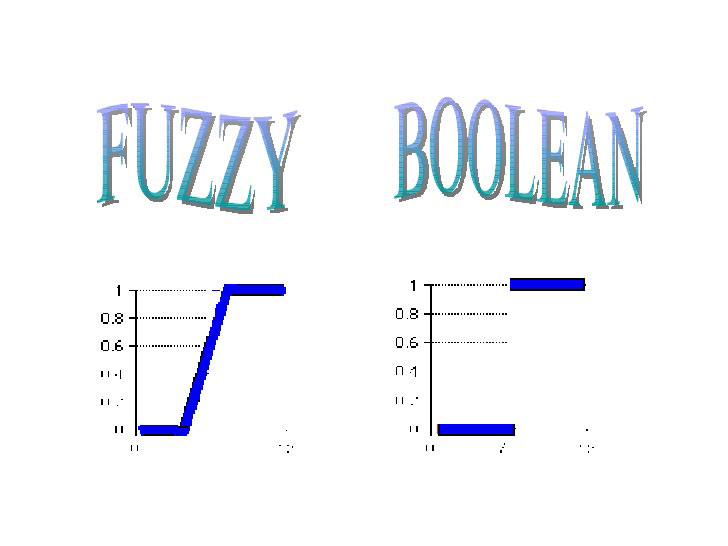
تاریخچه منطق فازی
منطق فازی یا Fuzzy Logic برای اولین بار در سال 1960 توسط دکتر لطفی زاده، استاد علوم کامپیوتری دانشگاه برکلی کالیفرنیا، ابداع شد.
مقاله کلاسیک پرفسور لطفیزاده درباره مجموعه فازی که در سال 1965 به چاپ رسید، سرآغاز جهتی نوین در علوم و مهندسی سیستم و کامپیوتر بود. پس از آن پرفسور لطفی زاده به پژوهشهای خود در زمینه مجموعه فازی ادامه داد تا آنکه در سال 1973 طی یک مقاله کلاسیک دیگر تحت عنوان “شرحی بر دیدی نو در تجزیه و تحلیل سیستمهای پیچیده و فرایندهای تصمیم گیری” مفهوم استفاده از متغیرهای زبانی را در سیستمهای حافظه و کنترل مطرح کرد. این مقاله اساس تکنولوژی کنترل بر مبنای منطق فازی است که در آینده اثرات عمیق در طراحی سیستمهای کنترل هوشمند خواهد داشت.
در سال 1975 ممدانی و اسیلیان چهارچوب اولیهای را برای کنترل کننده فازی مشخص کردند و کنترل کننده فازی را به یک موتور بخار اعمال نمودند. نتیجه در مقالهای تحت عنوان (آزمایشی در سنتز زبانی با استفاده از یک کنترل کننده فازی) منتشر گردید. در فوریه1992 اولین کنفرانس بین المللی IEEE در زمینه سیستمهای فازی در سان دیگو برگزار گردید.
این یک اقدام سمبلیک در مورد پذیرفتن سیستمهای فازی بوسیله بزرگترین سازمان مهندسی یعنی IEEE بود. در سال 1993 بخش سیستمهای فازی IEEE گشایش یافت. شرکت OMRON در سال 1993 اولين كامپيوتر مبتنی بر سيستم فازی را ساخت.
پرفسور لطفیزاده
لطفعلی رحیماوغلو عسکرزاده (زادهٔ ۱۵ بهمن ۱۲۹۹، برابر با ۴ فوریهٔ ۱۹۲۱ – در گذشته ۱۶ شهریور ۱۳۹۶، برابر با ۶ سپتامبر۲۰۱۷)، مشهور به لطفیزاده یا لطفی ع. زاده ریاضیدان، عالم کامپیوتر، مهندس برق و استاد بازنشسته علوم کامپیوتر در دانشگاه کالیفرنیا، برکلی، دانشمند سرشناس ایرانی-آمریکایی و مبدع نظریه سیستمهای فازی و شاخههای متنوع آن بود.
لطفیزاده از پدری ایرانی و مادری روس در باکو در جمهوری آذربایجان متولد شد و تحصیلات اولیه خود را در باکو و تهران انجام داد. او بیش از همه به خاطر طرح کردن ریاضیات فازی مشتمل بر مفاهیم مرتبط فازی همچون مجموعههای فازی، منطق فازی، الگوریتمهای فازی، کنترل فازی و احتمالات فازی شناخته شدهاست. گفته میشود نوآوریهای پروفسور لطفیزاده، امکانپذیری یک پارادایم تازه در هوش مصنوعی را تبیین، و رئوس کلی آن را ترسیم کردهاست.
مفاهیم اولیه در منطق فازی
منطق فازی يك نوع منطق است كه روش های نتيجه گيری در مغز بشر را جايگزين میكند. در واقع روشی است كه مغز انسان خود بر اساس آن كار میكند يعنی ورودیها و پردازش در مغز انسان فازی هستند. ما میتوانيم اين روش پردازش را در ماشينها هم پياده سازی كنيم تا آنها هم بتوانند آن را اجرا كنند و از فوايد آن بيشتر و بهتر استفاده كنيم.
سیستمهای منطقی فازی یک فرا مجموعه از منطق بولی است که بر مفهوم درستی نسبی، دلالت میکند. منطق کلاسیک هر چیزی را بر اساس یک سیستم دوتائی نشان میدهد (درست یا غلط، 0 یا 1، سیاه یا سفید) ولی منطق فازی درستی هر چیزی را با یک عدد که مقدار آن بین صفر و یک است نشان میدهد. مثلاً اگر رنگ سیاه را عدد صفر و رنگ سفید را عدد 1 نشان دهیم، آن گاه رنگ خاکستری عددی نزدیک به صفر خواهد بود.
منطق فازی معتقد است که ابهام در ماهیت علم است. بر خلاف دیگران که معتقدند که باید تقریبها را دقیقتر کرد تا بهرهوری افزایش یابد، لطفیزاده معتقد است که باید به دنبال ساختن مدلهایی بود که ابهام را به عنوان بخشی از سیستم معرفی کند.
یک مثال کاربردی مجموعههای فازی با مجموعههای کلاسیک
یکی از مثالهای پرکاربرد در زمینهی مجموعههای فازی، مجموعهی افراد بلند قد است. در این مورد مجموعه ما حاوی همهی اندازه قدهای ممکن از 1متر تا 2متر میباشد. همچنین کلمه بلند قد متناظر با معنایی است که درجهی بلند قدی هر فرد را مشخص میکند.
در صورتی که بخواهیم یک مجموعه کلاسیک برای انجام این طبقه بندی معرفی کنیم، میتوانیم بگوییم که همهی افراد بلندتر از 170سانتی متربلند قد هستند. اما این نوع طبقه بندی تا حد زیادی ناکارآمد میباشد، زیرا به عنوان مثال در دنیای واقعی نمیتوان یک فرد 170 سانتیمتری را بلند قد و دیگری را کوتاه قد نامید، درحالی که دومی فقط به اندازهی چند میلیمتر از اولی کوتاهتر میباشد.
مجموعه فازی افراد بلند قد
با توجه به ناکارآمدی طبقهبندی یاد شده میتوان مفاهیم ذهنی و واحدهای مختلف را در قالب مجموعههای فازی تعریف نمود. مثلا زمانی که شما میگویید «او بلند قد است» تابع عضویت باید سن و سال فرد مورد بحث را نیز در نظر بگیرد. (مثلا اینکه شما در مورد یک فرد 6 ساله صحبت میکنید یا یک فرد بالغ).
چرا سیستم فازی؟
دو نوع توجیه برای تئوری سیستمهای فازی وجود دارد:
دنیای واقعی ما بسیار پیچیده تر از آن است که بتوان یک توصیف و تعریف دقیق برای آن بدست آورد بنابراین باید یک توصیف تقریبی یا همان فازی که قابل قبول تجزیه و تحلیل باشد برای یک مدل معرفی شود.
با حرکت ما بسوی عصر اطلاعات، دانش و معرفت بشری بسیار اهمیت پیدا میکند. بنابراین ما به فرضیهای نیاز داریم که بتوان دانش بشری را به شکل سیستماتیک فرموله کرده و آن را به همراه سایر مدلهای ریاضی در سیستمهای مهندسی قرار دهد.
توجیه اول گرچه درست است با این حال طبیعت واحدی را برای تئوری سیستمهای فازی مشخص نمیکند. در حقیقت تمامی نظریههای علوم مهندسی دنیای واقعی را به شکلی تقریبی توصیف میکنند.یک تئوری مهندسی خوب از یکسو باید بتواند مشخصههای اصلی و کلیدی دنیای واقعی را توصیف کرده و از سویی دیگر قابل تجزیه تحلیل ریاضی باشد.
توجیه دوم مشخصه واحدی از سیستمهای فازی را توصیف کرده و وجودی تئوری سیستمهای فازی را به عنوان یک شاخصه مستقل در علوم مهندسی توجیه میکند. بعنوان یک قاعده کلی، یک تئوری مهندسی خوب باید قادر باشد از تمامی اطلاعات موجود به نحو موثری استفاده کند.
سیستمهای فازی چگونه سیستمهایی هستند؟
سیستمهای فازی سیستمها مبتنی بردانش یا قواعد میباشد. قلب یک سیستم فازی یک پایگاه دانش بوده که از قواعد اگر-آنگاه فازی تشکیل شده است. یک قاعده اگر-آنگاه فازی یک عبارت اگر-آنگاه بوده که بعضی کلمات آن بوسیله توابع تعلق پیوسته مشخص شدهاند.
بعنوان مثال اگر سرعت اتومبیل بالاست آنگاه نیروی کمتری به پدال گاز وارد کنید.
رفتار رانندگان در شرایط طبیعی شامل سه قاعده زیراست:
- اگر سرعت پایین است آنگاه نیروی بیشتری به پدال گاز وارد کنید.
- اگر سرعت متوسط است آنگاه نیروی متعادلی به پدال گاز وارد کنید.
- اگر سرعت بالاست آنگاه نیروی کمتری به پدال گاز وارد کنید.
کنترل کننده فازی
ما میتوانیم یک سیستم فازی را بر اساس این قواعد بسازیم. از آنجا که سیستم فازی بعنوان کنترل کننده استفاده شده. آن را کنترل کننده فازی مینامند. بطور خلاصه نقطه شروع ساخت یک سیستم فازی بدست آوردن مجموعهای از قواعد اگر-آنگاه فازی از دانش افراد خبره یا دانش حوزه مورد بررسی میباشد. مرحله بعدی ترکیب این قواعد در یک سیستم واحد است.
انواع سیستمهای فازی و مقایسه آنها
سيستم فازی روش توسعه يافته منطق بولی برای بكاربردن مفاهيم مبهم است. برای بيان ابهام در قالب يك عدد، سيستم فازی تابعی برای عضويت در يك دسته معرفی میكند، كه به هر عنصر يك عدد حقيقی بين صفر و يك نسبت میدهد(صفر و يك هم شامل اين اعداد میباشند). اين عدد نشان دهنده درجه عضويت عنصر نسبت به مجموعه مورد نظر میباشد.عضويت صفر بيانگر اين است كه عنصر مورد نظر كاملاً خارج از مجموعه است. درحاليكه عدد يك نشاندهنده اين است كه عنصر مورد نظر كاملاًدر مجموعه قرار دارد.
معمولا از سه نوع سیستم فازی صحبت به میان میآید:
- 1) سیستمهای فازی خالص
- 2) سیستمهای فازی تاکاگی – سوگنو و کانگ( TSK )
- 3) سیستمهای با فازی ساز و غیر فازی ساز (ممدانی)
سیستمهای فازی خالص
سیستم فازی خالص پایگاه قواعد فازی مجموعه ای از قواعد اگر-آنگاه فازی است. موتور استنتاج فازی این قواعد را به یک نگاشت از مجموعههای فازی در فضای ورودی به مجموعههای فازی در فضای خروجی بر اساس اصول منطق فازی ترکیب میکند. مشکل اصلی در رابطه با سیستمهای فازی خالص این است که ورودیها و خروجیهای آن مجموعههای فازی میباشند. در حالی که درسیستمهای مهندسی ورودی و خروجیها متغیرهایی با مقادیر حقیقی میباشند.
سیستمهای فازی تاکاگی – سوگنو و کانگ( TSK )
برای حل این مشکل تاکاگی _ سوگنو و کانگ نوع دیگری سیستمهای فازی معرفی کردهاند که ورودیها و خروجیهای آن متغییرهایی با مقادیر واقعی هستند. بدین ترتیب قاعده فازی از یک عبارت توصیفی با مقادیر زبانی،به یک رابطه ساده تبدیل شده است.
سیستمهای با فازی ساز و غیر فازی ساز (ممدانی)
به طور مثال اگر سرعت اتومبیل X باشد، انگاه نیروی وارد بر پدال گاز برابر است با Y=CX مقایسه نشان میدهد که بخش“ انگاه“ قاعده فازی از یک عبارت توصیفی با مقادیر زبانی به یک رابطه ریاضی ساده تبدیل شده این تغییر ترکیب قواعد فازی را ساده تر میسازد. در حقیقت سیستم فازی TSK یک میانگین وزنی از مقادیر بخشهای“ انگاه“ قواعد میباشد. مشکلات عمده سیستم فازی TSK عبارتند از:
- بخش“ آنگاه“ قاعده یک فرمول ریاضی بوده و بنابراین چهارچوبی را برای نمایش دانش بشری فراهم نمیکند.
- این سیستم دست ما را برای اعمال اصول مختلف منطق فازی باز نمیگذارد و در نتیجه انعطاف پذیری سیستمهای فازی در این ساختار وجود ندارد.
برای حل این مشکل ما از نوع سومی از سیستمهای فازی یعنی سیستمهای فازی با فازی ساز و غیر فازی ساز استفاده میکنیم. به منظور استفاده ازسیستمهای فازی خالص در سیستمهای مهندسی یک روش ساده اضافه کردن یک فازی ساز در ورودی که متغییرهایی با مقادیر حقیقی را به یک مجموعه فازی تبدیل کرده و یک غیر فازی ساز که یک مجموعه فازی را به یک متغییر با مقدار حقیقی در خروجی تبدیل میکند میباشد.
نتیجه یک سیستم فازی با فازی ساز و غیر فازی ساز است. این سیستم فازی معایب سیستم فازی خالص و سیستم فازی TSK را میپوشاند. از این پس منظور ما از سیستمهای فازی سیستمهای فازی با فازی ساز و غیر فازی ساز خواهد بود.
کاربردهای سیستم فازی
در اينجا به برخی از موارد كاربرد سيستمهای فازی اشاره میگردد.

- دستگاه تهويه مطبوع: دستگاه طوری تنظيم میشود تا به تدريج دمای اتاق به دمای مورد نظر برسد.
- دستگاه تنظيم سرعت: سرعت وسيله نقليه را با كاهش يا افزايش شتاب و همچنين كنترل سوخت و ترمز، بر روی مقدار ثابتی حفظ میكند.
- ديگ بخار كشتی: دما ، فشار و محتويات شيميايی را كنترل كرده و در سطح قابل اطمينانی قرار میدهد.
- دوربينهای فيلمبرداری: تشخيص میدهد كه شيئی كه از آن فيلمبرداری میشود حركت میكند يا حركت، ناشی از لرزش دست فيلمبردار است.
- ماشينهای لباسشويی: چرخه شستشو را با امتحان اندازه لباسها ، مقدار پودر لباسشويی و ميزان پاك كنندگی بهينه میكند.
- سيستمهای تشخيص تهاجم.
- پيش بينی زردی نوزاد.
- صنعت اتومبيل سازی.
- طراحی روباتی كه قادر به تشخيص رنگها باشد.
- ساخت كنترل كنندههای لوازم خانگی.
چند مثال از منطق فازی
ماشین شستشوی فازی
(چندین ورودی و یک خروجی)
سیستم فازی مورد استفاده یک سیستم سه ورودی یک خروجی است که سه ورودی فوق نوع کثیفی و مقدار اندازهگیری شده کثیفی وحجم لباس بوده و خروجی تعداد دورهای مناسب شستشو میباشد. بعنوان ورودی (سنسورهایی) در این سیستم تعبیه شده این سنسورها که از نوع نوری میباشند میزان نوری را که از طرف مقابل ساطع شده واز آب عبور کرده را اندازه گیری مینمایند.
سنسور نوری همچنین میتواند معین کند که نوع کثیفی چیست لباس گل آلود است یا چرب؟ گِل در آب سریعتر حل میشود بنابراین اگر نور دریافتی بسرعت کاهش پیدا کند در آن صورت لباس گل آلود است در حالی که اگر لباس روغنی باشد کندتر در آب حل شده و کاهش نور دریافتی کندتر خواهد بود.
ماشین همچنین دارای یک سنسور بار میباشد که حجم لباسها را ثبت میکند واضح است که تعداد لباسهای بیشتر زمان بیشتری برای شستشو لازم دارد. موارد فوق را میتوان در تعدادی قاعده اگر- آنگاه فازی برای ساخت یک سیستم فازی خلاصه کرد.
کنترل فازی کوره سیمان
(چند ورودی و چندخروجی)
سیمان بوسیله آسیاب کلینکر که ترکیبی از مواد معدنی است در یک کوره ساخته میشود. بدلیل این که عملکرد این کوره غیر خطی و متغییر با زمان میباشد ودادههای نمونه برداری کمی نیز دارد کنترل آن با استفاده از روشهای کنترل متعارف کاری مشکل است. در اواخر دهه 1970 شرکتی در دانمارک یک سیستم فازی را برای کنترل کوره سیمان ابداع نمود. سیستم فازی ابداعی چهار ورودی و دو خروجی داشت.
ورودیهای چهارگانه عبارتند از
- 1- درصد اکسیژن در گازهای اگزوز
- 2- درجه حرارت گازهای اگزوز
- 3- گشتاور آسیاب کوره
- 4- وزن حجمی کلینکر
خروجیهای این سیستم نیز عبارتند از
- میزان زغال سنگ ریخته شده به کوره
- میزان جریان هوا
- مجموعهی که از قواعد اگر-آنگاه فازی رابطه خروجیها را با ورودیها مشخص میکند. بعنوان مثال:
- اگر درصد اکسیژن بالا ودرجه حرارت پایین است آنگاه درجه هوا را افزایش دهید.
- اگر درصد اکسیژن بالا و درجه حرارت بالا است آنگاه میزان زغال سنگ را اندکی کاهش دهید.
بررسی روشهای چهارگانه استفاده از منطق فازی
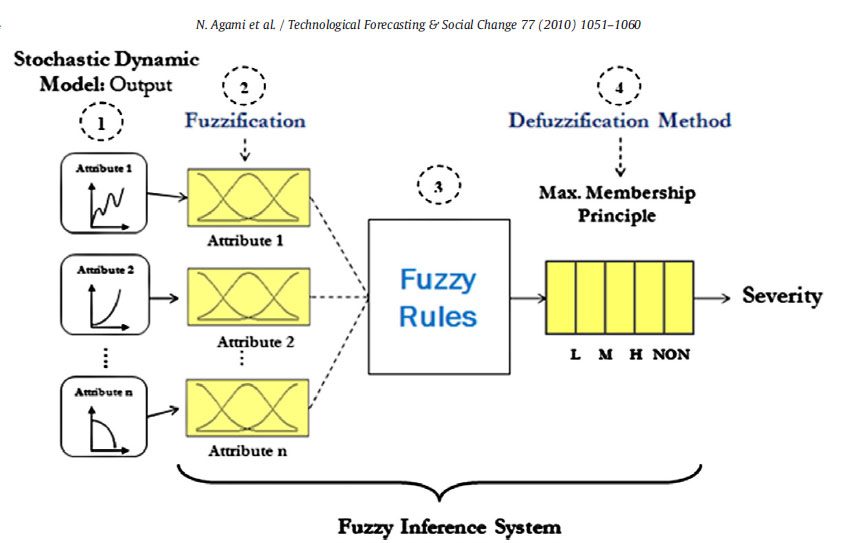
حال اين سوال مطرح است كه اين وسايل چگونه از منطق فازی استفاده میكنند؟
فازی كردن
در اين مرحله واقعيات بر اساس سيستم فازیتعريف میشوند. ابتدا بايد ورودی و خروجی سيستم معرفی شده، سپس قوانين اگر-آنگاه مناسب به كار گرفته شوند. برای ساخت تابع عضويت بايستی از داده های خام استفاده شود. حال سيستم برای اعمال منطق فازی آماده است.
مثالی برای فازی كردن
دستگاه تهويهای را در نظر بگيريد كه با اندازه گيری دما و رطوبت اتاق ميزان به جريان در آوردن هوا را مشخص میكند. در اين مورد ورودی عبارتست از دما و ميزان رطوبت وخروجی نيز سطح جريان هوای خروجی از دستگاه تهويه مطبوع است كه شامل سه حالت، خاموش، كم و زياد میباشد همچنين اين قوانين اگرـآنگاه استفاده میشوند:
- اگر اتاق گرم باشد آنگاه هوای زيادی منتشر كن
- اگر اتاق خنك باشد، آنگاه هيچ هوايی منتشر نكن
- اگر اتاق سرد و مرطوب است، آنگاه كمی هوا را به جريان بيينداز.
در آخر، متخصص بايد دو تابع عضويت تعيین كند. يكی برای اينكه دما را به مقدار فازی تبديل كند وديگری برای تبديل ميزان رطوبت به مقدار فازی.
استنتاج
هنگامی كه ورودیها به سيستم استنتاج میرسند، همه قوانين اگر-آنگاه را مورد ارزيابی قرار میدهد و ”درجه درستی“ آنها را مشخص میكند. اگر يك ورودی داده شده به طور صريح با يك قانون اگر-آنگاه مشخص نشده باشد، آنگاه تطابق بخشی مورد استفاده قرار میگيرد که دارای وزن بیشتر است تا جواب مشخص شود.
مثالی برای استنتاج
فرض كنيد دستگاه تهويه مطبوع دما و درجه رطوبت را اندازهگيری كرده و به آنها به ترتيب مقادير فازی 0.7 و 0.1 را نسبت داده باشد. حال اين سيستم بايستی درستی هر يك از قوانين فازی را كه در بالا بحث شد مورد بررسی قرار دهد. براي اين منظور روشهای استنتاج بسياری وجود دارد. اين مثال ساده ترين روش را مورد استفاده قرار میدهد كه روش ماكسيمم-مينيمم ناميده میشود.
اين روش مقدار فازی قسمت آنگاه (نتيجه) را به قسمت اگر نسبت میدهد. بنابراين اين روش مقادير فازی 0.7 و 0.1 و 0.1 را به ترتيب به قوانين 1، 2 و 3 نسبت میدهد.
پایگاه قواعد
در اين قسمت برای بدست آوردن يك نتيجه كلی تمامی مقادير بدست آمده از قسمت استنتاج با هم تركيب میشوند. قوانين فازی مختلف نتايج مختلفی خواهند داشت. بنابراين ضروری است تا همه قوانين در نظر گرفته شوند.
مثالی برای پایگاه قواعد
هر نتيجه استنتاجی درباره سيستم تهويه مطبوع عمل خاصی را پيشنهاد میكند. در مثال فوق قانون اول، سطح گردش هوای زياد را پيشنهاد میكند. قانون دوم، خاموش كردن، و قانون سوم، سطح گردش هوای كم را بيان میكند. تكنيكهای متعددی برای بدست آوردن نتيجه كلی وجود دارند. اين مثال از روش ماكزيمم-مينيمم كه روش سادهای است استفاده میكند.
اين روش ماكزيمم مقدار فازی قسمت استنتاج به عنوان نتيجه در نظر میگيرد. يعنی در عمل، قسمت ساخت مقدار 0.7 را انتخاب میكند چون مقدار بيشتری را بين مقادير فازی دارا است.
غیرفازی ساز
در اين مرحله مقدار فازی بدست آمده از قسمت پایگاه قواعد به يك داده قابل استفاده تبديل میشود. اين قسمت از كار اغلب پيچيده است چون مجموعه فازی نبايستی مستقيما به داده قابل استفاده تبديل شود. از آنجا كه كنترلگرهای سيستمهای فيزيكی به سيگنالهای گسسته نياز دارند، اين مرحله بسيار مهم میباشد.
مثالی برای غیر فازی ساز
به خاطر داريد كه مقدار فازی بدست آمده از مرحله قبل 0.7 بود. اين مقدار عددی برای سيستم تهويه مطبوع قابل فهم نيست. بايد مشخص شود كه دستگاه كداميك از فرامين كم، زياد يا خاموش را به جريان بيندازد. مرحله بازگرداندن از حالت فازی بايستی عدد 0.7 را به يكی از فرامين فوق تبديل كند. در اين مثال واضح است كه مقدار خروجی 0.7 بيانگر اين است كه سيستم تهويه مطبوع بايستی در حالت زياد باشد.
دلایل استفاده از منطق فازی
میتوان دلایل استفاده گسترده از منطق فازی را در موارد ذیل خلاصه نمود:
- – منطق فازی از نظر مفهومی بسیار ساده میباشد، زیرا مفاهیم ریاضی مورد استفاده در استدلال فازی بسیار ساده هستند.
- – منطق فازی بسیار انعطاف پذیر است. در واقع به آسانی میتوان یک سیستم فازی را برای حل یک مسله جدید سازماندهی نمود و نیازی به طراحی دوباره سیستم وجود ندارد.
- – منطق فازی دارای قابلیت مدل سازی توابع غیر خطی پیچیده میباشد. میتوانید برای برقراری ارتباط بین هر مجموعه از دادههای ورودی و خروجی از سیستم فازی استفاده کنید. این فرایند از طریق تکنیکهایی نظیر تکنیک ANFIS بسیار ساده میشود.
- – منطق فازی توان تحمل دادههای غیر دقیق فازی را به شکل مطلوبی دارا میباشد. با نگاه دقیق به هرچیزی، متوجه نوعی نادرستی در آن میشویم و منطق فازی از این مفهوم یک پردازش سازمان یافته میسازد.
- – منطق فازی بر مبنای تجربه متخصصان عمل میکند. برخلاف شبکههای عصبی که دادههای آموزشی را دریافت کرده و مدلهای مبهم تولید میکند، منطق فازی به شما اجازه میدهدتا بر تجربه متخصصانی که شناخت دقیقی از سیستم مورد بررسی دارند، تکیه نمایید.
- – منطق فازی با تکنیکهای کنترلی مرسوم قابل ادغام است. سیستمهای فازی الزاما جایگزینی برای روشهای کنترلی نیستند، بلکه در بسیاری از موارد سیستمهای فازی پیاده سازی سیستمهای کنترلی را تکمیل و تسهیل میکنند.
- – منطق فازی بر مبنای زبان طبیعی میباشد. اصول منطق فازی بر مبنای نوع ارتباط بشر است. از آنجا که منطق فازی بر پایه ساختارهای توصیف کیفی در زبان روزمره استوار است، استفاده از آن بسیار ساده میباشد.
- مورد آخر شاید مهمترین مورد بوده و سزاوار بحث بیشتری است. زیرا زبان طبیعی که توسط مردم در امور روزمره مورد استفاده قرار میگیرد بر مبنای تاریخ هزاران ساله زندگی بشر شکل گرفته و بهینه سازی شده است.
کمبودها و نواقص سیستمهای فازی
منطق فازی و منطق بولی هر دو بر پايه واقعيات میباشند. با اين تفاوت كه منطق فازی توانايی كاركردن با دادههای مبهم را نيز داراست. با اين وجود منطق فازی هنوز قادر به حل بعضی مسائل نيست.
بسياری از سيستمها، مانند آنچه در بحث كاربرد گفته شد میتوانند از منطق فازی بدون هيچ مشكلی استفاده كنند. چون نياز به هيچ تصميم گيری درونی و فكری ندارند. اما بعضی سيستمها به منطق پيچيدهتری نياز دارند تا بتوانند به بيان گمان، تعقل ، شك و … بپردازند.
براي نشان دادن نقصان منطق فازی میتوان به سيستم شناخت دوست يا دشمن اشاره كرد
اين سيستم برای شناخت هواپيماهای ارتشی يا مسافربری دوست و دشمن به كار میرود. در حالت عادی سيستم از هر هواپيما يك سيگنال شناسايی دريافت میكند. دلايل زيادی وجود دارند كه ممكن است سيستم اين سيگنال را دريافت نكند مانند: بد عمل كردن سيستم، بد عمل كردن فرستنده، نبودن اين سيستم روی هواپيماها، پارازيت سيگنال يا خاموش بودن راديو.
در اين موارد، اين سيستم بايد از منطق برای شناسايی هواپيماها استفاده كند. كه فقط مربوط به دادههای از قبيل مسير پرواز نيست. چون اين دادهها هواپيماهای دوست را از دشمن تشخيص نمیدهند. بنابراين منطق فازی در سيستم تشخيص دوست از دشمن كاربردی ندارد! برای اين منظور بايد از منطقی استفاده شود كه توانايی تصميم گيری درونی را داشته باشد.
چه زمانی نباید از منطق فازی استفاده نمود؟
منطق فازی همیشه یک راه حل مناسب نیست، اما چه زمانی نباید از آن استفاده کرد؟ همانطور که میدانید منطق فازی یک روش مناسب و آسان برای نگاشت فضای ورودی به فضای خروجی است. حال اگر در یک مسالهای متوجه شدید که استفاده از منطق فازی چندان ساده نیست، بهتر است به دنبال راه حل دیگری بروید. بسیاری ازکنترل کنندهها، بدون کمک منطق فازی به خوبی عمل میکنند.
جعبه ابزار منطق فازی در MATLAB
جعبه ابزار منطق فازی متشکل از مجموعهای از توابع فازی در قالب محیط محاسباتی MATLAB میباشد. این جعبه ابزار امکاناتی را برای استنتاج سیستمهای فازی در چارچوب MATLAB فراهم میآورد. همچنین در راستای شبیه سازی سیستمهای فازی، امکان یک پارچه سازی آنها در قالب نرم افزار Simulink وجود دارد. میتوانید از توابع مربوط به این جعبه ابزار در برنامههای دیگر (مثلا به زبانC) استفاده نمایید. این جعبه ابزار از یک محیط گرافیکی برای کمک به کاربر بهره میگیرد، اما در صورت تمایل میتوانید از توابع مربوط به آن روی خط فرمان MATLAB استفاده نمایید.
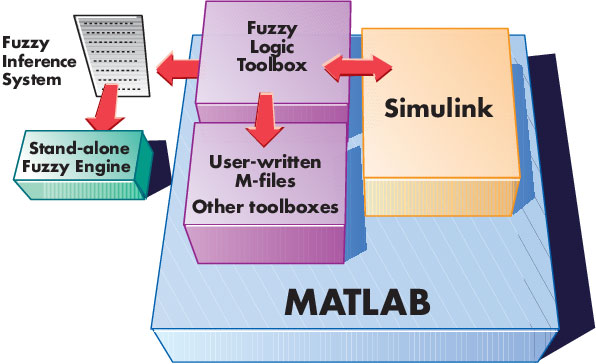
این جعبه ابزار دارای سه دسته متفاوت از امکانات میباشد:
- – توابع خط فرمان،
- – توابع محاورهای گرافیکی،
- – بلوکهای Simulink،
دستهی اول از توابعی تشکیل میشود که میتوانید آنها را روی خط فرمان و یا از برنامه کاربردی خود فراخوانی نمایید. بسیاری از این توابع در قالب M-Fileهای MATLAB پیاده سازی شدهاند. در واقع الگوریتمهای مربوط به منطق فازی به وسیلهی دستورات MATLAB در قالب این فایلها پیاده سازی شدهاند. برای مشاهده کد مربوط به این توابع، از دستور زیر روی خط فرمان استفاده نمایید.
Type function_name
میتوانید با اعمال تغییر در هر یک از توابع مربوط به جعبه ابزار و ذخیره سازی مجدد آن با یک نام جدید، توابع مورد نظر خود را ساخته و قابلیتهای این جعبه ابزار را گسترش دهید.
در دسته دوم، جعبه ابزار مجموعهای از ابزارهای محاورهای را برای دسترسی کاربر از طریق محیط گرافیکی به ابزارهای مختلف فراهم میآورد. این ابزارهای گرافیکی محیطی را برای طراحی، تحلیل و پیاده سازی سیستمهای فازی فراهم میآورند.
دسته سوم امکانات این جعبه ابزار، از مجموعهای از بلوکهای Simulink تشکیل شده اند که برای شبیه سازی سریع سیستمهای فازی در قالب محیطSimulink به کار میروند.
با توجه به اینکه غالب استدلالهای بشر با قواعد فازی مرتبط هستند، اهمیت و کاربرد این جعبه ابزار روز به روز در حال گسترش میباشد. این جعبه ابزار با فراهم آوردن یک چارچوب نظاممند برای محاسبات مربوط به قواعد فازی، به شکل مطلوبی قدرت استدلال کاربر را افزایش میدهد.
نحوه عملکرد جعبه ابزار منطق فازی
به کمک جعبه ابزار منطق فازی MATLAB ، میتوان سیستمهای استنتاج فازی را ایجاد و ویرایش کرد. میتوانید اینکار را از طریق ابزارهای گرافیکی و توابع خط فرمان انجام دهید. همچنین امکان ایجاد این سیستمها به صورت خودکار از طریق تکنیکهای کلاسترینگ و انطباقی neuro-fuzzy وجود دارد. همچنین در صورتی که به نرم افزار Simulink دسترسی داشته باشید، میتوانید سیستم فازی خود را از طریق بلوکهای Simulink شبیه سازی کنید.
همچنین این جعبه ابزار، قابلیت اجرای برنامههای C را به صورت مستقیم به شما میدهد این عملیات به کمک موتور استنتاج فازی ممکن میشود. میتوانید این موتور را برای کاربرد مورد نظر خود سفارشی کنید.
جعبه ابزار منطق فازی در MATLAB
به دلیل یکپارچه بودن محیط MATLAB میتوانید ابزارهای مورد نظر خود را برای پیاده سازی یک سیستم فازی به کمک جعبه ابزارهای مختلف مثل سیستمهای کنترلی، شبکههای عصبی و یا جعبه ابزار بهینه سازی فراهم آورید.
منابع:
ویکی پدیا





