tic-tac-toe یا دوز رو احتمالا خیلی از دوستان بشناسند، یک بازی پرطرف دار قدیمی است که مکانیسم ساده ای دارد. این بازی ۲ نفره است و در آن بازیکن ها سعی میکنند سه مهره خود را به ردیف در جایگاه ها بنشانند و در این صورت پیروز خواهند بود. ردیف های افقی یا عمودی یا مورب فرقی نخواهد داشت و هر کدام باعث پیروزی در بازی خواهد شد. حریف سعی خواهد کرد با قرار دادن مهره های خود جلوی ردیف شدن ۳ مهره از شما را بگیرد. در قسمت اول از آموزش هوش مصنوعی شطرنج الگوریتم minmax را توضیح دادیم و به شکل فرضی نحوه عملکرد آن را توضیح دادیم. در این قسمت سعی خواهیم کرد به شکل عملی با پیاده سازی عملی بازی دوز (tic-tac-toe) نشان دهیم چطور میتوان با استفاده از این الگوریتم یک رقیب خوب (در واقع رقیبی که حرکات حساب شده دارد) پیاده سازی کرد. با ما همراه باشید!
مختصری در باره بازی tic-tac-toe
بازی tic-tac-toe مدلهای مختلفی دارد، مدل ۱۲ تایی یا ۶ تایی یا ۹ تایی سری ۱۲ تایی از همه سختتر است و نیاز به تمرکز زیادی دارد، در این آموزش ما سادهترین نوع دوز را پیاده سازی خواهیم کرد! چرا که هم تعداد حالتهایی که نیاز به پردازش دارند کمتر هستند و مدل برنامه سادهتر و قابلدرکتر خواهد بود مخصوصاً برای هدف ما که آشنایی بیشتر با الگوریتم minmax است و هم این که مرسومتر است و احتمالاً اغلب دوستان یک بار این بازی را تجربه کردهاند.

همانطور که در تصویر مشخص است، در این بازی ۹ جای خالی وجود دارد که هر بازیکن مهره خود را به نوبت در هر کدام از موقعیتها که دوست دارد قرار میدهد بازیکنها باید سعی کنند که مهرههای خود (سه مهره) را در یک راستای عمودی یا افقی یا مورب قرار دهند، در صورت بروز چنین حالتی بازیکن برنده بازی خواهد بود مثل عکس زیر:
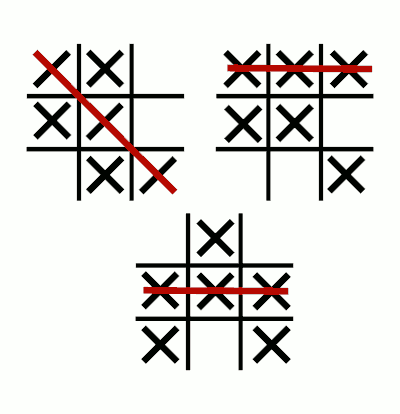
تیک تاک تویی نام های دیگری مثل ایکس او یا Noughts and Crosses نیز دارد.
همینطور میتوانید بهصورتآنلاین آن را بازی کنید.
از کجا شروع کنیم؟ زمین!
قرار است با استفاده از الگوریتم minmax یک هوش مصنوعی برای بازی tic-tac-toe پیاده سازی کنیم که حالتهای ممکن را در نظر گرفته و بهترین حرکت ممکن را انجام دهد، برای این کار اول لازم است که کامپیوتر یا میکروکنترلر از زمین بازی درک درستی داشته باشد، از آنجایی که ما قرار است ۹ مکان برای نگهداری مهرهها داشته باشیم برای تعریف زمین بازی میتوانیم به سادگی از یک آرایه ۳ در ۳ استفاده کنیم، البته روش بهینهتری برای ذخیره زمین بازی وجود دارد ولی از آنجایی که مقاله بیشتر جنبه آموزشی دارد ما سعی خواهیم کرد سادهترین حالت ممکن را در نظر بگیریم.
میدانیم که هر خانه از زمین بازی میتواند ۳ حالت داشته باشد، یا خالی است یا مهره بازیکن X در آن است یا مهره بازیکن O در خانههای آن قرار دارد. پس قبل از تعریف زمین لازم است متغیری را تعریف کنیم که وضعیت هر خانه از زمین را نمایش دهد. برای این کار از enum استفاده میکنیم. در نهایت تعریف زمین بازی به شکل زیر خواهد بود.
typedef enum
{
cell_free = 0,
cell_player_X,
cell_player_O,
}BoardCell_t;
BoardCell_t board[3][3] =
{
{ cell_free, cell_free, cell_free },
{ cell_free, cell_free, cell_free },
{ cell_free, cell_free, cell_free }
};
حالا که زمین بازی را تعریف کردیم، نیاز است که بتوانیم برد را چاپ کنیم (نمایش دهیم) برای این کار هم تابع زیر را به شکلی که میبینید مینویسم:
void print_board(BoardCell_t board[3][3])
{
char Pbrod[] = {'_','X','O'};
printf("\r\n\tTic Tac Toe\r\n\r\n");
printf("Player 1 (X) - Player 2 (O)\r\n\r\n\r\n");
printf(" | | \n");
printf(" %c | %c | %c \n", board[0][0], board[0][1], board[0][2]);
printf("_____|_____|_____\n");
printf(" | | \n");
printf(" %c | %c | %c \n", board[1][0], board[1][1], board[1][2]);
printf("_____|_____|_____\n");
printf(" | | \n");
printf(" %c | %c | %c \n", board[2][0], board[2][1], board[2][2]);
printf(" | | \n\n");
}
فکر میکنم تابع فوق عملکردش به اندازه کافی روشن است و نیاز به توضیح خاصی ندارد. این تابع متغیری تحت عنوان زمین بازی از ما دریافت میکنید و آن را به شکلی که قابل درک برای ما باشد نمایش میدهد. در نهایت تابع خروجی به شکل زیر خواهد داشت.
Tic Tac Toe Player 1 (X) - Player 2 (O) | | O | | _____|_____|_____ | | | X | _____|_____|_____ | | | | | |
آیا بازی تمام شده است
گام بعدی برای پیاده سازی هوش مصنوعی این است که چک کنیم ببینیم آیا بازی تمام شده است یا نه، همانطور که قبلاً توضیح دادهام در الگوریتم minmax ما باید تمام حالتهای ممکن را چک کنیم و حالتی که بیشترین امتیاز را نسیب ما میکنید را انتخاب کنیم، برای این که بتوانیم تمام حالتهای ممکن را چک کنیم نیاز است بدانیم آیا زمین بازی جای خالی برای حرکت جدید دارد یا نه! خوب پیاده سازی این تابع هم مثل قبلیها ساده است تنها کافی است چک کنیم و ببینیم آیا موقعیت خالی در زمان بازی وجود دارد یا نه! تابع آن به شکل زیر خواهد بود.
bool IsMovesLeft(BoardCell_t board[3][3])
{
for (int i = 0; i<3; i++)
for (int j = 0; j<3; j++)
if (board[i][j]==cell_free)
return true;
return false;
}
عملکرد تابع بسیار ساده است، تکتک خانههای بازی را چک میکند، اگر خانهای خالی مانده باشد پس هنوز میتوان حرکت جدیدی انجام داد و به همین دلیل تابع مقدار true برمیگرداند.
آیا کسی برنده شده است
همانطور که در قسمت قبل گفتیم، در الگوریتم minmax ما دو بازیکن داریم یکی حداکثرکننده و دیگری حداقلکننده، در انجام حرکتهای مختلفی که هرکدام از بازیکنها انجام میدهند باید قادر باشند که بررسی کنند آیا حرکتی که انجام دادهاند فارغ از این که باعث تمام شدن بازی شده است یا خیر باعث برد یا باخت رقیب شده است یا نه، یعنی نیاز داریم که تابعی داشته باشیم که با بررسی زمین بازی بتواند بگوید کدام بازیکن برنده شده است و یا این که هیچ کدام برنده نشده است.
در واقع این تابع با توجه به وضعیت مهرهها ارزیابی میکند کدام بازیکن برنده شده است یا این که هنوز بازی هیچ برندهای ندارد، این تابع بسته به نوع بازی به شکلهای مختلفی نوشته میشود و اتفاقاً نوع نوشتن این تابع در هوش نمایش داده شده از برنامه تأثیر مستقیم دارد. ایده اولیه پشت این تابع آن است که برای حداکثرکننده مقدار مثبت خروجی دهد و برای بازیکن حداقلکننده مقدار منفی، و اگر هیچ کدام از بازیکنها برنده نبودند خروجی صفر (بی طرف) برگرداند. در این سناریو ما فرض میکنیم که بازیکن X یک بازیکن حداکثرکننده است و بازیکن O بازیکن حداقلکننده است. خوب بیایید تابع رو بنویسیم:
۱. اگر بازیکن X (حداکثر کننده) برنده بازی باشد تابع ما مقدر مثبت ۱۰ را بر میگرداند.
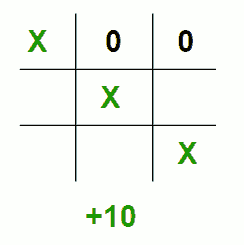
۲. اگر بازیکن O (حداقلکننده) برنده بازی باشد تابع ما مقدار منفی ۱۰ را بر میگرداند.
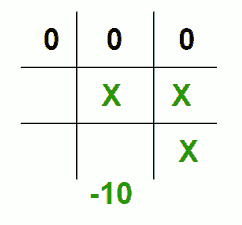
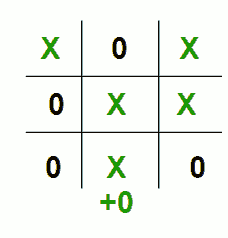
int BoardEvaluate(BoardCell_t board[3][3])
{
// Checking for Rows for X or O victory.
for (int row = 0; row<3; row++)
{
if (board[row][0]==board[row][1] && board[row][1]==board[row][2])
{
if (board[row][0]==cell_player_X)
return +10;
else if (board[row][0]==cell_player_O)
return -10;
}
}
// Checking for Columns for X or O victory.
for (int col = 0; col<3; col++)
{
if (board[0][col]==board[1][col] && board[1][col]==board[2][col])
{
if (board[0][col]==cell_player_X)
return +10;
else if (board[0][col]==cell_player_O)
return -10;
}
}
// Checking for Diagonals for X or O victory.
if (board[0][0]==board[1][1] && board[1][1]==board[2][2])
{
if (board[0][0]==cell_player_X)
return +10;
else if (board[0][0]==cell_player_O)
return -10;
}
if (board[0][2]==board[1][1] && board[1][1]==board[2][0])
{
if (board[0][2]==cell_player_X)
return +10;
else if (board[0][2]==cell_player_O)
return -10;
}
// Else if none of them have won then return 0
return 0;
}
تابع حرکت ساز
تا اینجا فکر میکنم همه چیز روشن باشد حالا با توجه به ماهیت عملکردی تابع مینمکس نیاز است که بتوانیم حرکتهای مختلفی را ایجاد کنیم بعد با استفاده از تابع ارزیابی امتیاز آن حرکت را ارزیابی کنیم. تابع حرکت ساز نقش مهمی در میزان هوش برنامه بازی میکند، البته در بازی tic-tac-toe پیاده سازی این تابع خیلی ساده است چرا که هیچ قاعده خاصی برای حرکت مهرهها وجود ندارد و تنها کافی است که جای خالی را پیدا کنیم و مهره مورد نظر را در آن قرار دهیم ولی در بازیهای پیچیدهتر مثل شطرنج یکی از مهمترین توابعی که وجود خواهد داشت همین تابع است. در بازی شطرنج مهرهها باید طبق قاعده بازی حرکت کنند و هر مهره الگو (pattern) حرکتی منحصر به فرد خود را دارد و آنجاست که اهمیت این تابع مشخص میشود.
با توجه به این که عملکرد این تابع به عملکرد تابع minmax گره خورده است چرا که باید هر حرکت محتمل را وزن دهی کنیم، تابع را تنها به شکل شبه برنامه پیاده سازی کنیم و در ادامه کد دقیق آن را بنویسیم.
function findBestMove(board): bestMove = NULL for each move in board : if current move is better than bestMove bestMove = current move return bestMove
همانطور که مشخص است عملکرد این تابع زیاد هم پیچیده نیست، تمام حرکتهای ممکن را میسنجیم و میبینیم که کدام حرکت امتیاز بیشتری در بر خواهد داشت که نهایتاً همان حرکت را انجام خواهیم داد.
محاسبه امتیاز هر حرکت (minmax)
خوب حالا میرسیم به قسمت چالشی هوش مصنوعی، چطور امتیاز یک حرکت را باید حساب کنیم؟، برای این کار نیاز است برنامه به نوعی با خودش بازی را ادامه دهد یعنی به سعی کند عکسالعمل شما را حدس بزند و ببینید آیا این حرکتی که انجام داده است آیا باعث پیروزیاش در بازی میشود یا خیر! این کار به شکل تابع برگشتی انجام میدهیم مکانیسمی مثل پیاده سازی تابع فاکتوریل!
همانطور که میدانید که در الگوریتم مینمکس دو بازیکن وجود دارد یکی در تلاش برای زیاد کردن امتیاز و دیگری برای تلاش برای کم کردن امتیاز است! برای این که بتوانیم به شکل بازگشتی (سادهتر) از این تابع استفاده کنیم نیاز نیست دوتابع مختلف بنویسیم تنها کافی است که نوع بازیکن را به شکل پارامتر در ورودی دریافت کنیم. به شبه کد زیر دقت کنید:
function minimax(board, depth, isMaximizingPlayer): if current board state is a terminal state : return value of the board if isMaximizingPlayer : bestVal = -INFINITY for each move in board : value = minimax(board, depth+1, false) bestVal = max( bestVal, value) return bestVal else : bestVal = +INFINITY for each move in board : value = minimax(board, depth+1, true) bestVal = min( bestVal, value) return bestVal
همانطور که در شبه کد میبینید مثلاً برای کاربر حداکثر کننده ما از منفیترین مقدار ممکن شروع به سنجش حرکتهای ممکن (تابع ایجاد حرکت) میکنیم و همیشه به دنبال بیشترین امتیاز ممکن هستیم. در قیمت حداقل کننده از مثبتترین امتیاز ممکن شروع میکنیم و به دنبال کم کردن امتیاز هستیم. بعد از انجام یک حرکت مجدداً خود تابع را صدا میزنیم برای تخمین حرکت بازیکن مقابل.
بگذارید برای روشن شدن بیشتر عملکرد تابع با تصویر عملکرد شبه کد را نمایش دهیم.
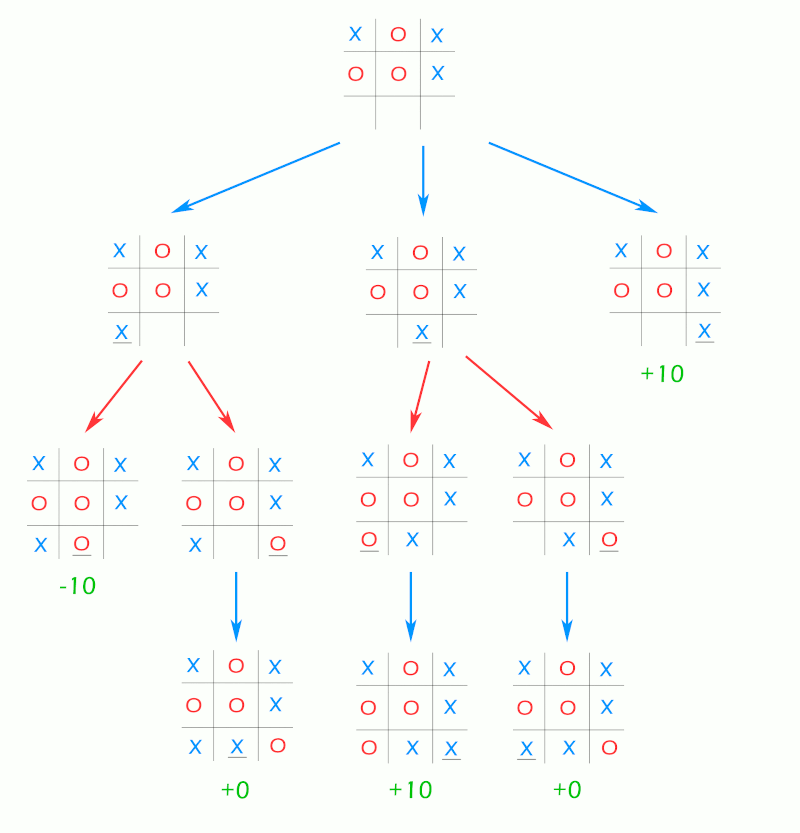
در بالاترین سطر بازیکن حداقل کننده (O) بازی کرده و حالا نوبت بازیکن حداکثر کننده است (X) سه موقعیت خالی وجود دارد که میتواند در آنها بازی کند (پایینترین ردیف بازی) پس بازیکن حداکثرکننده (X) مهره خود را در هر موقعیت قرار داده و بررسی میکنید در هر کدام از موقعیتها احتمال برد بیشتر است.
حداکثرکننده پس بعد از هر انتخاب تابع minmax را برای حداقل کننده (O) فراخوانی میکند و تا او بازی را با قواعد خودش انجام دهد و بعد مجدداً تابع minmax را برای بازیکن حداکثرکننده صدا میزند و این فرایند تا تمام شدن تمام حالتهای ممکن ادامه پیدا میکند و امتیازها محاسبه میشود و از بین امتیازها حرکتی انتخاب میشود که بالاترین امتیاز را داشته باشد.
کمی هوشمندتر
به مسائل بالا دقت کنید، اگر بازیکن حداکثرکننده (X) مهره خودش رو وسط یا سمت راست بذار توی هر کدام از حالتها امکان برنده شدن هست، یعنی امتیازش میشه +۱۰ ولی اگر وسط رو انتخاب کنه به احتمال ۵۰ درصد ممکنه بازی رو نبره! و بازی مساوی بشه که اون ۵۰ درست بستگی به نحوه بازی حداقلکننده (O) داره، یا این که بازی طوری پیش بره که توی هر دو احتمال امکان برنده شدن وجود داشته باشه و هیچ مساویای هم در کار نباشد ولی برای برنده شدن در یک حالت اول نیاز به ۲ حرکت باشه در حالت دوم نیاز به ۴ حرکت باشد! منطقیتر هست که با ۲ حرکت بازی را برنده شویم به جای ۴ حرکت، اما چطور میشود چنین چیزی را پیاده سازی کرد؟ ساده است اینجا ما میتوانیم تعداد حرکات رو در الگوریتم محاسبه امتیاز در نظر بگیریم هر حرکت اضافه (عمق بیشتر) امتیاز منفی در بر خواهد داشت، که به عبارتی میشود برای حداکثرکننده (X) و امتیاز مثبت خواهد داشت برای حداقل کننده (O) با این شرایط برنامه سعی خواهد کرد در سریعترین حالت ممکن بازی را برنده شود.
if maximizer has won: return WIN_SCORE – depth else if minimizer has won: return LOOSE_SCORE + depth
در انتها برنامه به شکل زیر خواهد بود
#include <stdio.h>
#include <stdbool.h>
#define max(a, b) \
( \
{ \
typeof(a) _a = (a); \
typeof(b) _b = (b); \
_a > _b ? _a : _b; \
})
#define min(a, b) \
( \
{ \
typeof(a) _a = (a); \
typeof(b) _b = (b); \
_a < _b ? _a : _b; \
})
typedef enum
{
cell_free = ' ',
cell_player_X = 'X',
cell_player_O = 'O',
} BoardCell_t;
typedef struct
{
int row, col;
} move_t;
// This function print the board
void print_board(BoardCell_t board[3][3])
{
printf("\r\n\tTic Tac Toe\r\n\r\n");
printf("Player 1 (O) - Player 2 (X)\r\n\r\n\r\n");
printf(" | | \n");
printf(" %c | %c | %c \n", board[0][0], board[0][1], board[0][2]);
printf("_____|_____|_____\n");
printf(" | | \n");
printf(" %c | %c | %c \n", board[1][0], board[1][1], board[1][2]);
printf("_____|_____|_____\n");
printf(" | | \n");
printf(" %c | %c | %c \n", board[2][0], board[2][1], board[2][2]);
printf(" | | \n\n");
}
// This function returns true if there are moves
// remaining on the board. It returns false if
bool IsMovesLeft(BoardCell_t board[3][3])
{
for (int i = 0; i < 3; i++)
for (int j = 0; j < 3; j++)
if (board[i][j] == cell_free)
return true;
return false;
}
// Returns a value based on who is winning
// b[3][3] is the Tic-Tac-Toe board
int BoardEvaluate(BoardCell_t board[3][3])
{
// Checking for Rows for X or O victory.
for (int row = 0; row < 3; row++)
{
if (board[row][0] == board[row][1] && board[row][1] == board[row][2])
{
if (board[row][0] == cell_player_X)
return +10;
else if (board[row][0] == cell_player_O)
return -10;
}
}
// Checking for Columns for X or O victory.
for (int col = 0; col < 3; col++)
{
if (board[0][col] == board[1][col] && board[1][col] == board[2][col])
{
if (board[0][col] == cell_player_X)
return +10;
else if (board[0][col] == cell_player_O)
return -10;
}
}
// Checking for Diagonals for X or O victory.
if (board[0][0] == board[1][1] && board[1][1] == board[2][2])
{
if (board[0][0] == cell_player_X)
return +10;
else if (board[0][0] == cell_player_O)
return -10;
}
if (board[0][2] == board[1][1] && board[1][1] == board[2][0])
{
if (board[0][2] == cell_player_X)
return +10;
else if (board[0][2] == cell_player_O)
return -10;
}
// Else if none of them have won then return 0
return 0;
}
// This is the minimax function. It considers all
// the possible ways the game can go and returns
// the value of the board
int minimax(BoardCell_t board[3][3], int depth, bool isMax)
{
int score = BoardEvaluate(board);
// If Maximizer has won the game return his/her
// evaluated score
if (score == 10)
return score - depth;
// If Minimizer has won the game return his/her
// evaluated score
if (score == -10)
return score + depth;
// If there are no more moves and no winner then
// it is a tie
if (IsMovesLeft(board) == false)
return 0;
// If this maximizer's move
if (isMax)
{
int best = -1000;
// Traverse all cells
for (int i = 0; i < 3; i++)
{
for (int j = 0; j < 3; j++)
{
// Check if cell is empty
if (board[i][j] == cell_free)
{
// Make the move
board[i][j] = cell_player_X;
// Call minimax recursively and choose
// the maximum value
best = max(best, minimax(board, depth + 1, !isMax));
// Undo the move
board[i][j] = cell_free;
}
}
}
return best;
}
// If this minimizer's move
else
{
int best = 1000;
// Traverse all cells
for (int i = 0; i < 3; i++)
{
for (int j = 0; j < 3; j++)
{
// Check if cell is empty
if (board[i][j] == cell_free)
{
// Make the move
board[i][j] = cell_player_O;
// Call minimax recursively and choose
// the minimum value
best = min(best, minimax(board, depth + 1, !isMax));
// Undo the move
board[i][j] = cell_free;
}
}
}
return best;
}
}
// This will return the best possible move for the player
move_t findBestMove(BoardCell_t board[3][3])
{
int bestVal = -1000;
move_t bestMove;
bestMove.row = -1;
bestMove.col = -1;
// Traverse all cells, evaluate minimax function for
// all empty cells. And return the cell with optimal
// value.
for (int i = 0; i < 3; i++)
{
for (int j = 0; j < 3; j++)
{
// Check if cell is empty
if (board[i][j] == cell_free)
{
// Make the move
board[i][j] = cell_player_X;
// compute evaluation function for this
// move.
int moveVal = minimax(board, 0, false);
// Undo the move
board[i][j] = cell_free;
// If the value of the current move is
// more than the best value, then update
// best/
if (moveVal > bestVal)
{
bestMove.row = i;
bestMove.col = j;
bestVal = moveVal;
}
}
}
}
printf("my move is Col:%d - Row %d\r\n", bestMove.col, bestMove.row);
return bestMove;
}
move_t GetUserMove()
{
int Ucode = 0;
do
{
printf("Enter your move (1~9):");
scanf("%d", &Ucode);
if (!(Ucode > 0 && Ucode < 10))
printf("you must be entered value between 1~9\r\n");
} while (!(Ucode > 0 && Ucode < 10));
Ucode--;
move_t usermove;
usermove.row = 2 - (Ucode / 3);
usermove.col = (Ucode % 3);
return usermove;
}
bool MoveAction(BoardCell_t board[3][3], move_t move, BoardCell_t player)
{
/*check this position for free*/
if (board[move.row][move.col] != cell_free)
return false;
board[move.row][move.col] = player;
return true;
}
int main()
{
BoardCell_t board[3][3] = {
{cell_free, cell_free, cell_free},
{cell_free, cell_free, cell_free},
{cell_free, cell_free, cell_free}};
int Evaluate = 0;
print_board(board);
while (1)
{
move_t user = GetUserMove();
if (!MoveAction(board, user, cell_player_O))
{
/*check for end game*/
if (!IsMovesLeft(board))
break;
printf("You can't use this location\r\nThis location has already been used!\r\n");
continue;
}
move_t ai = findBestMove(board);
if (ai.col != -1)
MoveAction(board, ai, cell_player_X);
else
break;
print_board(board);
/*check for winner*/
Evaluate = BoardEvaluate(board);
if (Evaluate != 0)
break;
}
if (Evaluate == 0)
printf("\r\n\tThe game equalised\r\n");
else if (Evaluate > 0)
printf("\r\n\tMe Won :)\r\n");
else
printf("\r\n\tyou Won! :(\r\n");
return 0;
}
سورس کد برنامه را برای STM32f030f4 میتوانید از گیت هاب دانلود کنید.
منبع:سیسوگ





