مدارات DC قسمت چهارم: قوانین مدار کیرشهف

قوانین مدار کیرشهف به ما امکان می‌دهد با تعریف مجموعه‌ای از قوانین و قضیه‌های اساسی شبکه برای ولتاژها و جریان‌های اطراف مدار، مشکلات پیچیده مدار را حل کنیم. در آموزش مقاومت‌ها دیدیم که وقتی دو یا چند مقاومت هر دو سری، موازی یا ترکیبی از هر دو به هم متصل می‌شوند، یک مقاومت معادل (R_T) پیدا می‌شود و این مدارها از قانون اهم پیروی می‌کنند.

بااین‌حال، گاهی اوقات در مدارهای پیچیده مانند شبکه‌های Bridge یا T، نمی‌توانیم به‌سادگی از قانون اهم برای یافتن ولتاژها یا جریان‌های گردش یافته در مدار استفاده کنیم. برای این نوع محاسبات به قوانین خاصی نیاز داریم که به ما امکان می‌دهد معادلات مدار را به‌دست آوریم و برای این امر می‌توانیم از قانون‌مدار کیرشهف استفاده کنیم.

در سال 1845 یک فیزیکدان آلمانی، گوستاو کیرشهف یک جفت یا مجموعه‌ای از قواعد یا قوانین تهیه کرد که مربوط به محافظت در جریان و انرژی در مدارهای الکتریکی است.

این دو قانون معمولاً به این صورت شناخته می شوند:

قوانین مدار کیرشهف، یکی از قوانین کیرشهف که با جریان در حول مداربسته سروکار دارد، قانون جریان کیرشهف (KCL) است، درحالی‌که قانون دیگر با منابع ولتاژ موجود در یک مداربسته، قانون ولتاژ کیرشهف (KVL) است.

قانون اول کیرشهف-قانون جریان (KCL)

قانون جریان کیرشهف یا KCL، اظهار می‌دارد که جریان کل یا شارژ واردشده به یک محل اتصال یا گره دقیقاً برابر است با شارژ خارج‌شده از گره، زیرا محل دیگری برای خارج شدن ندارد، زیرا هیچ الکترونی در گره از بین نمی‌رود به‌عبارت‌دیگر، مجموع جبری تمام جریانهای ورودی و خروجی به یک گره باید برابر با صفر باشد، I_(exiting) + I_(entering) = 0 این ایده توسط کیرشهف معمولاً به‌عنوان Conservation of Charge شناخته می‌شود.

قانون جریان کیرشهف

در اینجا سه جریان ورودی به گره I1،I2،I3 ازنظر ارزش مثبت هستند و دو جریان I4 و I5 خارج‌شده از گره، ازنظر ارزش منفی هستند. سپس این بدان معنی است که ما می‌توانیم معادله را دوباره بنویسیم:

I₁ + I₂ + I₃ – I₄ – I₅ = 0

اصطلاح گره در یک مدار الکتریکی به‌طورکلی به ارتباط یا اتصال دو یا چند مسیر حمل جریان یا عناصر مانند کابل‌ها و اجزا اشاره دارد. همچنین برای شارش جریان درون گره یا خارج از آن باید مسیر مداربسته وجود داشته باشد. ما می‌توانیم هنگام تجزیه‌وتحلیل مدارهای موازی از قانون جریان کیرشهف استفاده کنیم.

قانون دوم کیرشهف- قانون ولتاژ (KVL)

قانون ولتاژ کیرشهف یا KVL، اظهار می‌دارد که “در هر شبکه حلقه بسته، ولتاژ کل اطراف حلقه برابر است با مجموع افت ولتاژ درون همان حلقه” که این نیز برابر با صفر است. به‌عبارت‌دیگر مجموع جبری تمام ولتاژهای داخل حلقه باید برابر با صفر باشد. این ایده توسط کیرشهف به‌عنوان Conservation of Energy شناخته می‌شود.

قانون ولتاژ کیرشهف

شروع در هر نقطه از حلقه در همان جهت ادامه پیدا می‌کند و جهت تمام افت ولتاژها، مثبت یا منفی بودن آن ولتاژ را ذکر می‌کند و دوباره به همان نقطه شروع بازمی‌گردد. مهم است که جهت یکسانی در جهت عقربه‌های ساعت یا خلاف جهت عقربه‌های ساعت حفظ شود وگرنه مقدار ولتاژ نهایی برابر با صفر نخواهد بود. ما می‌توانیم هنگام تجزیه‌وتحلیل مدارهای سری از قانون ولتاژ کیرشهف استفاده کنیم.

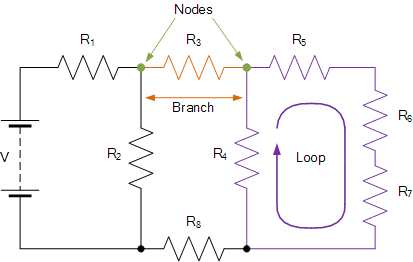
هنگام تجزیه‌وتحلیل مدارهای DC یا مدارهای AC با استفاده از قوانین مدار کیرشهف، از تعدادی تعریف و اصطلاحات برای توصیف قسمتهای مدار مورد تجزیه‌وتحلیل استفاده می‌شود مانند: گره، مسیرها، شاخه‌ها، حلقه‌ها و مش‌ها.

اصطلاحات رایج نظریه مدار DC 

• مدار: مدار یک مسیر هدایت حلقه بسته است که در آن جریان الکتریکی شارش دارد.
• مسیر: یک خط واحد از عناصر یا منابع اتصال‌دهنده.
• گره: گره محل اتصال، ارتباط یا ترمینال در مدار است که دو یا چند عنصر مدار به هم مرتبط یا به متصل شده‌اند و نقطه اتصال را بین دو یا چند شاخه ایجاد می‌کنند. یک گره با یک نقطه نشان داده می‌شود.
• شاخه: شاخه یک یا گروهی از اجزا مانند مقاومت یا منبع است که بین دو گره متصل می‌شوند.
• حلقه: یک حلقه یک مسیر بسته ساده در مدار است که در آن هیچ عنصر یا گره مدار بیش از یک بار مشاهده نمی‌شود.
• مش: مش یک مسیر سری حلقه بسته است که هیچ مسیر دیگری را شامل نمی‌شود، هیچ حلقه‌ای در داخل مش وجود ندارد.

توجه داشته باشید که:
اگر مقدار جریان یکسانی در تمام اجزا شارش داشته باشد، گفته می‌شود قطعات به‌صورت سری به هم متصل می‌شوند.
اگر مقدار ولتاژ یکسانی به دو سر قطعات اعمال شود، گفته می‌شود قطعات به‌صورت موازی به هم متصل می‌شوند.

یک مدار DC معمولی

مثال قانون جریان کیرشهف، جریان را در مقاومت 40Ω ،R3 پیدا کنید:

مدار دارای 3 شاخه، 2 گره (A و B) و 2 حلقه مستقل است.

با استفاده از قانون جریان کیرشهف، معادلات KCL به شرح زیر است:

At node A :    I₁ + I₂ = I₃

At node B :    I₃ = I₁ + I₂

با استفاده از قانون ولتاژ dvait، معادلات KVL به شرح زیر است:

Loop 1 is given as :    10 = R₁ I₁ + R₃ I₃ = 10I₁ + 40I₃

Loop 2 is given as :    20 = R₂ I₂ + R₃ I₃ = 20I₂ + 40I₃

Loop 3 is given as :    10 – 20 = 10I₁ – 20I₂

از آنجا که I₃ حاصل جمع I₁ + I₂ است، می‌توانیم معادلات را دوباره بنویسیم.

Eq. No 1 :    10 = 10I₁ + 40(I₁ + I₂)  =  50I₁ + 40I₂

Eq. No 2 :    20 = 20I₂ + 40(I₁ + I₂)  =  40I₁ + 60I₂

اکنون دو “معادله چند مجهولی” داریم که می‌تواند با کاهش آن‌ها مقادیر I₁ و I₂ را کاهش دهد.

تعویض I₁ از نظر I₂، مقدار I₁ را 0.143- آمپر می‌دهد.

تعویض I₂ از نظر I₁، مقدار I₂ را 0.429+ آمپر می‌دهد.

As :  I₃ = I₁ + I₂

جریان جاری در مقاومت R3 به صورت زیر ارائه می‌شود:

-0.143 + 0.429 = 0.286 Amps

و ولتاژ مقاومت R3 به این صورت داده می‌شود:

0.286 x 40 = 11.44 volts

علامت منفی برای I₁ به این معنی است که جهت جریان فعلی در ابتدا اشتباه بوده است، در واقع باتری 20 ولت در حال شارژ کردن باتری 10 ولت است.

کاربرد قوانین مدار کیرشهف

این دو قانون، جریان‌ها و ولتاژهای موجود در یک مدار را فراهم می‌سازد به‌عنوان‌مثال مدار “تجزیه‌وتحلیل” می‌شود، و روش اصلی استفاده از قوانین مدار کیرشهف به شرح زیر است:

1. فرض کنید تمام ولتاژها و مقاومت‌ها داده‌شده است. (در صورت عدم وجود برچسب V1، V2،… R1، R2 و غیره)
2. به هر شاخه یا مش یک جریان اختصاص دهید. (در جهت عقربه‌های ساعت یا در خلاف جهت عقربه‌های ساعت)
3. هر شاخه را با جریان شاخه‌ای برچسب بزنید. (I1، I2، I3 و غیره)
4. معادلات قانون اول کیرشهف را برای هر گره پیدا کنید.
5. معادلات قانون دوم کیرشهف را برای هر یک از حلقه‌های مستقل مدار پیدا کنید.
6. برای یافتن جریان‌های ناشناخته از معادلات چند مجهولی خطی استفاده کنید.

همچنین با استفاده از قانون‌مدار کیرشهف برای محاسبه ولتاژها و جریان‌های مختلفی که در اطراف یک مدار خطی گردش می‌کنند، می‌توان از تجزیه‌وتحلیل حلقه برای محاسبه جریان‌های موجود در هر حلقه مستقل استفاده کرد که به کاهش ریاضیات موردنیاز با استفاده از قوانین کیرشهف کمک می‌کند. در آموزش بعدی در مورد مدارهای DC، ما برای انجام این کار به بررسی تجزیه‌وتحلیل جریان مش می‌پردازیم.

منبع

منبع:سیسوگ