فهرست مطالب
-
هارمونیک ها
-
فرکانس اصلی
-
توالی هارمونیک
-
خلاصه
هارمونیک ها، فرکانسهای بالاتر ناخواستهای هستند که روی شکل موج اصلی سوار میشوند و یک الگوی موج اعوجاجی ایجاد میکنند.
در یک مدار AC، یک مقاومت ( رزیستانس ) دقیقا همان رفتاری را دارد؛ که در مدار DC دارد. به اینمعنا، که جریانی که از مقاومت عبور میکند؛ متناسب با ولتاژ موجود در آن است. زیرا مقاومت یک عنصر خطی است و اگر ولتاژ واردشده به آن، موج سینوسی باشد؛ جریان عبوری از آن نیز، موج سینوسی است و از اینرو، اختلاف فاز بین دوموج سینوسی صفر است.
معمولا، هنگام کار با ولتاژها و جریانهای متناوب، در مدارهای الکتریکی، فرض بر این است؛ که آنها خالص و سینوسی بوده و فقط یک مقدار فرکانس دارند؛ که “فرکانس اساسی” نام دارد اما همیشه این موضوع مطرح نیست.
در یک مدار یا دستگاه الکتریکی یا الکترونیکی با یک مشخصهی جریان ولتاژ غیرخطی، به این معنا که جریان عبوری از آن متناسب با ولتاژ اعمالشده نیست؛ شکلموج متناوب مرتبط با دستگاه، تا حدی بیشتر یا کمتر متفاوت از شکلموج سینوسی ایدهآل خواهد بود؛ این نوع شکلموج، معمولا به شکل شکلموج غیرسینوسی یا پیچیده شناخته میشود.
شکلموجهای پیچیده، توسط دستگاههای الکتریکی متداول، مانند سلفهای هسته آهن، ترانسفورماتورهای سوئیچینگ، بالاستهای الکترونیکی در چراغهای فلورسنت و دیگر دستگاهها مانند بارهای القایی سنگین، همانطورکه شکلموجهای ولتاژ و جریان خروجی AC در آلترنتورها، ژنراتورها و دیگر دستگاهها مانند ماشینهای الکتریکی تولید میشود.
همچنین، بیشتر مدارهای سوئیچینگ منبع تغذیه الکترونیکی، مانند یکسوسازها، یکسوسازیهای کنترلشده سیلیکونی ( SCR’s )، ترانزیستورهای توان، مبدلهای توان و دیگر مدارها، مانند سوئیچهای حالت جامد، توان تامینکننده شکلموج سینوسی را قطع میکنند تا موتور توان را کنترل کنند یا منبع سینوسی AC را به DC تبدیل نمایند. این مدارهای سوئیچینگ، فقط در مقادیر پیک منبع تغذیه AC جریان میکشند و از آنجایی که شکلموج جریان سوئچینگ، غیرسینوسی است؛ جریان بار حاصل حاوی هارمونیک است.
شکلموجهای پیچیده غیرسینوسی، با “جمع” مجموعهای از فرکانسهای موج سینوسی شناحتهشده به عنوان “هارمونیکها” ساخته میشوند. هارمونیک، اصطلاح عمومی است؛ که برای توصیف اعوجاج شکلموج سینوسی با شکلموجهای فرکانسهای مختلف استفاده میشود.
از اینرو، شکلموج پیچیده به هرشکلی که باشد؛ میتواند از نظر ریاضی، به عناصر جداگانه خود تقسیم شود که فرکانس اساسی و تعداد “فرکانس هارمونیک” نامیده میشود. اما منظور از “فرکانس اصلی” چیست؟
فرکانس اصلی
شکلموج بنیادی ( یا هارمونیک اول ) شکلموج سینوسی است؛ که فرکانس منبع را دارد. فرکانس بنیادی، پایینترین فرکانس یا فرکانس پایه ( f ) است؛ که شکلموج پیچیده بر روی آن ساخته شدهاست و به همینترتیب، دوره تناوب ( T ) شکلموج پیچیده حاصل، با دورهتناوب فرکانس اصلی برابر خواهد بود.
شکلموج اصلی یا هارمونیک اول بهصورت زیر نشان داده میشود:

درجاییکه، Vmax، مقدار پیک برحسب ولت است و f فرکانس شکلموج برحسب هرتز ( Hz ) است.
میتوان دید؛ که شکلموج سینوسی یک ولتاژ متناوب ( یا جریان )؛ بهعنوان یک تابع سینوسی با زاویه 2πf تغییر میکند. فرکانس شکلموجها ( f ) باتعداد سیکلها بر ثانیه تعیین میشود. در انگلستان، این فرکانس اساسی برابر با 50Hz است؛ درحالیکه در آمریکا برابر با 60Hz میباشد.
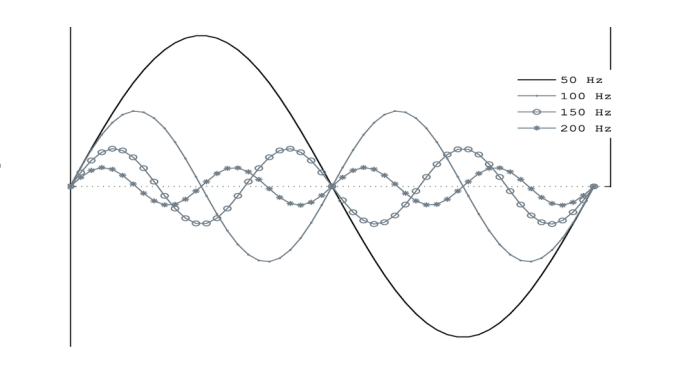
هارمونیک ها ولتاژها یا جریان هایی هستند که با فرکانسی کار میکنند که یک عدد صحیح (عدد کامل) از فرکانس اساسی است. پس اگر فرض کنیم؛ که شکلموج اساسی فرکانس 50Hz داشتهباشد؛ به این معناست که فرکانس هارمونیک دوم 100Hz( 2*50Hz )، هارمونیک سوم 150Hz( 3*50Hz )، هارمونیک پنجم، 250Hz و هارمونیک هفتم، 350Hz بوده و همینطور ادامه خواهد یافت. به همینترتیب، برای شکلموج اساسی 60Hz، فرکانسهای هارمونیک دوم، سوم، چهارم و پنجم، بهترتیب 120Hz ،180Hz ،240Hz و 300Hz خواهد بود. بنابراین، به عبارتدیگر، میتوان گفت که “هارمونیک ها”، مضربی از فرکانس اساسی بوده و میتواند به صورت 2f،3f و 4f و … مانند زیر نشان داده شود.

باید توجه داشت؛ که شکلموج قرمز رنگ در بالا، شکل واقعی شکلموج بوده که توسط یک بار مشاهده شدهاست؛ که بهدلیل محتوای هارمونیک به فرکانس اصلی اضافه میشود. شکلموج اصلی را میتوان شکلموج هارمونیک اول، نیز نامید. بنابراین، هارمونیک دوم دارای فرکانس دو برابر فرکانس اصلی است؛ هارمونیک سوم، دارای فرکانسی سهبرابر فرکانس اصلی و هارمونیک چهارم، چهاربرابر فرکانس اصلی است؛ که در سمت چپ نشان داده شدهاست.
سمتراست شکلموج پیچیدهای را نشان میدهد؛ که درنتیجه، اثر افزودن شکلموج اصلی و شکلموج هارمونیک در فرکانسهای مختلف هارمونیک، ایجاد شدهاست. باید توجه داشت؛ که شکلِ شکلموج پیچیدهی حاصل، نهتنها به تعداد و دامنه فرکانسهای هارمونیک موجود، بلکه به رابطهفاز بین فرکانس اصلی یا پایه و فرکانسهای هارمونیکی منفرد نیز بستگی دارد.
میتوان دید که یک موج پیچیده، از یک شکلموج بنیادی، بهعلاوه هارمونیک تشکیل شدهاست؛ هرکدام دارای مقدار پیک و زاویهفاز مخصوص به خود میباشند. اگر فرکانس اساسی بهصورت E = Vmax(2πƒt) باشد؛ مقادیر هارمونیک ها بهصورت زیر خواهد بود:
برای هارمونیک دوم

برای هارمونیک سوم

برای هارمونیک چهارم

و همینگونه ادامه خواهد داشت.
پس معادلهی دادهشده برای مقدار یک شکلموج پیچیده خواهد بود:

هارمونیکها، درحالت کلی، با نام و فرکانس خود طبقهبندی میشوند؛ بهعنوان مثال، یک هارمونیک دوم با فرکانس اصلی 100Hz و دنبالهآن طبقهبندی میشود. دنبالهی هارمونیک، به دوران فازوری ولتاژها و جریانهای هارمونیکی، باتوجه به شکلموج اصلی متعادل شده یک سیستم سهفاز چهار سیمه اشاره دارد.
یک هارمونیک دنبالهی مثبت ( ۱۰،۷،۴ و ….) همجهت ( مستقیم ) با فرکانس اساسی دوران مییابد؛ درجاییکه، یک هارمونیک دنبالهی منفی ( ۸،۵،۲ و …) در جهت مخالف ( معکوس ) فرکانس اساسی دوران مییابد.
بهطورکلی، هارمونیکهای دنبالهی مثبت، نامطلوب بوده؛ زیرا سبب گرمشدن بیش از حد هادیها، خطوط توان و ترانسفورماتورها، بهدلیل اضافهشدن شکلموج میگردند. از طرف دیگر، هارمونیکهای دنبالهی منفی، بین فازها دوران یافته و باعث ایجاد مشکل میشود؛ زیرا دوران فاز مخالف، میدان مغناطیسی دوار موردنیاز موتورها و بهویژه موتورهای القایی را تضعیف کرده و باعث تولید گشتاور مکانیکی کمتری میشود.
یک مجموعهدیگر خاص، بهنام “سهگانه” ( ضرب در سه ) دارای دنباله دورانی صفر است. سهگانهها، مضرب هارمونیک سوم میباشند (سوم، ششم، نهم و …) و بههمین دلیل اینگونه نامگذاری شدهاند و با صفردرجه جابهجا میشوند. هارمونیک دنباله صفر، بین فاز و مکان خنثی یا زمین در گردش است.
برخلاف هارمونیکهای دنبالهی مثبت و منفی که یکدیگر را خنثی میکنند؛ هارمونیکهای مرتبه سوم یا سهگانه خنثی نمیشوند. در یک سیم خنثی مشترک که از هر سهفاز تحت جریان قرار میگیرد؛ باهم جمع میشوند. نتیجه این است؛ که دامنهجریان در سیم خنثی، بهدلیل اینکه، هارمونیکهای سهگانه میتواند تا سه برابر دامنه جریان فاز در فرکانس اساسی باشد؛ باعث کارایی کمتر و بیش از حدگرم شدن میگردد.
میتوانیم اثرات دنباله را بهصورت چندبرابر شدن فرکانس اساسی ۵۰ هرتز خلاصه کنیم:
توالی هارمونیک

باید توجه داشت؛ که همان دنباله هارمونیکی برای شکلموجهای اساسی 60Hz نیز اعمال میشود.

خلاصه
هارمونیکها، فرکانسهای بالاتری هستند که روی فرکانس اصلی ( فرکانس مدار ) سوار میشوند و باعث اعوجاج شکلموج میگردند. میزان اعوجاج اعمالشده به موج اساسی، کاملا به نوع، کمیت و شکل هارمونیکهای موجود بستگی خواهد داشت.
هارمونیکها، از زمان معرفی درایوهای الکترونیکی، برای موتورها، فنها و پمپها، مدارهای سوئیچینگ منبع تغذیه؛ مانند یکسوسازها، مبدلهای برق و کنترلکنندههای توان تریستور و همچنین اکثر بارهای کنترلی فاز غیرخطی الکترونیکی و چراغهای فلورسنت فرکانس بالا ( صرفهجویی در انرژی ) در طی چند دهه اخیر، به مقدار کافی وجود داشتهاند. دلیل این امر، این است؛ که جریان کنترلشده توسط بار، مانند فرم یکسوسازها یا مدارهای سوئیچینگ نیمههادی توان، صادقانه از شکلموجهای سینوسی پیروی نمیکنند.
هارمونیکها در سیستم توزیع توان الکتریکی با فرکانس اصلی ( 50Hz و 60Hz ) تامین میشوند و باعث ایجاد اعوجاج در شکلموج ولتاژ و/یا جریان میشوند. این اعوجاج، یک شکلموج پیچیده با تعداد زیادی فرکانس هارمونیک ایجاد میکند؛ که میتواند بر تجهیزات الکتریکی و خطوط برق اثر سو بگذارد.
مقدار اعوجاج به شکلموج صورت مشخصی میبخشد که بهصورت مستقیم مرتبط با فرکانسها و اندازههای غالب عناصر هارمونیک است؛ که فرکانس هارمونیک آنها، چندبرابر ( تمام اعداد صحیح ) یک فرکانس اصلی است. غالبترین عناصرهارمونیک، هارمونیکهای مرتبه پایین دوم تا نوزدهم میباشند که سهگانهها از همه بدتر میباشند.
منبع:ردرونیک