فهرست مطالب
-
اتصال موازی مقاومت ها
-
مدار مقاومت موازی
-
معادله مقاومت موازی
-
شبکههای مختلف مقاومت موازی
-
جریان در مدار مقاومت موازی
-
خلاصه اتصال موازی مقاومتها
هنگامی که هر دو ترمینال یک مقاومت به دو ترمینال مقاومت دیگر متصل شود، گفته میشود که مقاومتها به طور موازی به یکدیگر متصل شدهاند. برخلاف مدار مقاومت سری، در شبکه مقاومت موازی جریان مدار میتواند بیش از یک مسیر را طی کند زیرا مسیرهای متعددی برای عبور وجود دارد. پس مدارهای موازی به عنوان تقسیم کنندههای جریان طبقه بندی میشوند.
از آنجا که مسیرهای متعددی برای عبور جریان تغذیه وجود دارد، ممکن است جریان تمام شاخههای شبکه موازی یکسان نباشد. با این حال، افت ولتاژ تمام مقاومتها در یک شبکه مقاومت موازی یکسان است. پس مقاومتهای موازی دارای ولتاژ مشترک در سرتاسر خود هستند و این برای همه عناصر موازی صادق است.
بنابراین می توانیم مدار مقاومتی موازی را به عنوان مداری تعریف کنیم که در آن همه مقاومتها به دو نقطه (یا گره) مشخص متصل میشوند و با این مشخصه شناسایی میشود که بیش از یک مسیر برای عبور جریان دارد که به یک منبع ولتاژ مشترک متصل است. پس در مثال مقاومت موازی زیر، ولتاژ مقاومت R۱ برابر است با ولتاژ مقاومت R۲ که برابر ولتاژ R۳ و ولتاژ تغذیه است. بنابراین، ولتاژ در یک شبکه مقاومت موازی به شرح زیر است:
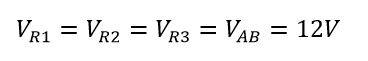
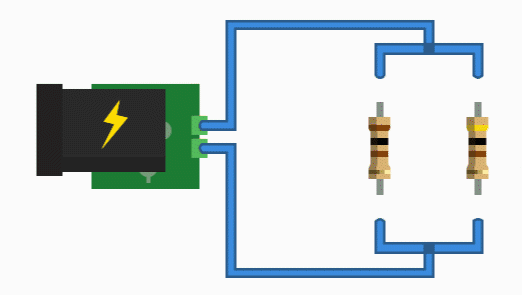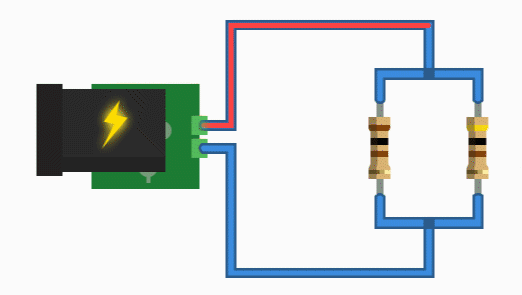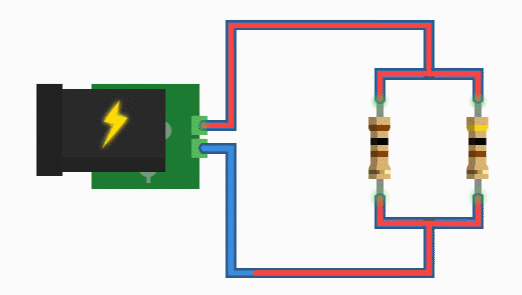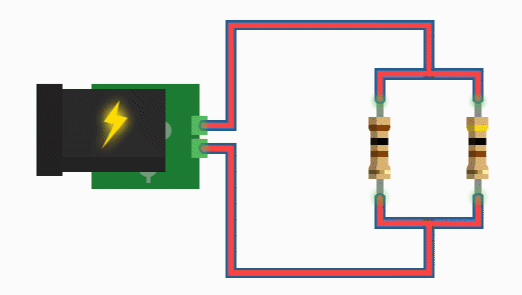
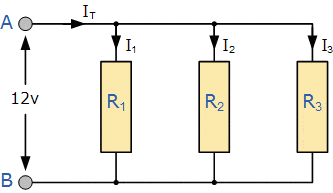
همانطور که در مدار شکل زیر نشان داده شده، مقاومتهای R۱، R۲ و R۳ به طور موازی بین دو نقطه A و B به هم متصل شدهاند.
مدار مقاومت موازی
در بخش قبل مشاهده کردیم که مقاومت کل RT در یک مدار سری برابر است با مجموع مقادیر مقاومتها. برای مقاومتهای موازی، محاسبه مقدار مقاومت معادل RT متفاوت است.
در اینجا، وارونه مقدار مقاومتها (1/R) با هم جمع میشوند و سپس مقاومت معادل، از معکوس کردن حاصل این جمع جبری به دست میآید.
معادله مقاومت موازی
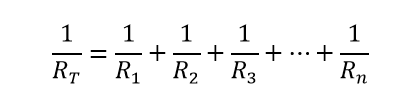
پس معکوس مقاومت معادل دو یا چند مقاومت موازی، مجموع جبری وارونه مقادیر تک تک مقاومتها است.
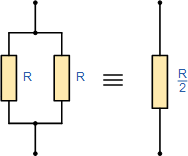
اگر دو مقاومت یا امپدانس موازی، برابر و از یک مقدار باشند، مقاومت معادل RT برابر با نصف مقدار یک مقاومت، یعنی R/2 است. برای سه مقاومت یا بیشتر، این مقدار به ترتیب برابر با R/3، R/4 و… میباشد.
توجه داشته باشید که مقاومت معادل همواره از کوچکترین مقاومت در شبکه موازی، کمتر است؛ بنابراین مقاومت کل RT، با افزودن مقاومتهای موازی اضافی همیشه کاهش مییابد.
مقاومت موازی مقداری را به ما میدهد که به عنوان رسانایی با نماد G شناخته میشود و واحد آن زیمنس با نماد S است. رسانایی معکوس مقاومت است (G = 1/R). برای تبدیل رسانایی به مقدار مقاومت، باید معکوس رسانایی را به دست آوریم که مقاومت کل RT را در اتصال موازی مقاومتها به ما میدهد.
اکنون می دانیم به مقاومتهایی که بین دو نقطه مشخص به متصل شده باشند، موازی گفته میشود. اما یک مدار مقاومت موازی میتواند اشکال دیگری به غیر از مدار شکل بالا داشته باشد. در اینجا چند نمونه از چگونگی اتصال موازی مقاومتها آمده است.
شبکههای مختلف مقاومت موازی
پنج شبکه مقاومتی زیر ممکن است از نظر ظاهری با یکدیگر متفاوت باشند، اما همه آنها به اشکال مختلف اتصال موازی مقاومتها هستند و به همین ترتیب شرایط و معادلات مذکور در آنها صادق است.
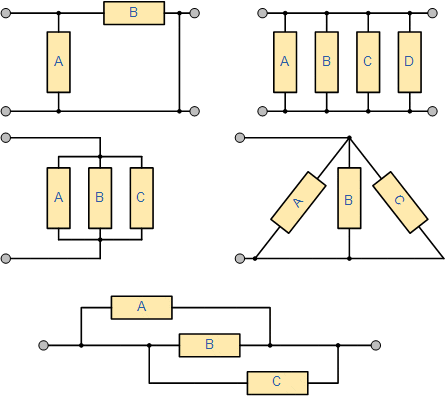
مثال ۱
مقاومت کل RT را در شبکه موازی زیر به دست آورید.
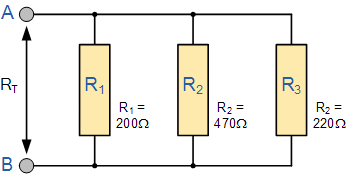
مقاومت کل RT بین دو ترمینال A و B به صورت زیر محاسبه میشود:
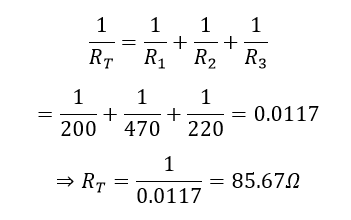
میتوان از این روش برای محاسبه مقاومت کل یک شبکه موازی با هر تعداد مقاومتی استفاده کرد.
اما اگر تنها دو مقاومت موازی وجود داشته باشد، میتوانیم از یک فرمول سادهتر و سریعتر برای یافتن مقدار مقاومت کل RT استفاده کنیم و از محاسبات اعداد وارونه بکاهیم.
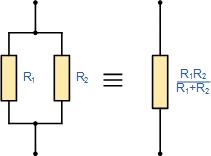
این روش بسیار سریعتر محاسبه معادل دو مقاومت موازی با مقادیر برابر یا نا برابر، که به عنوان «ضرب به جمع» شناخته میشود، به شرح زیر است:
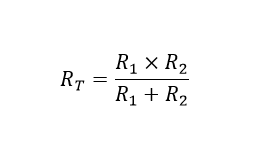
مثال ۲
مدار زیر را، که تنها دو مقاومت موازی دارد، در نظر بگیرید.
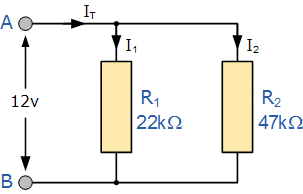
با استفاده از فرمول بالا برای دو مقاومت که به صورت موازی به هم متصل شدهاند، میتوانیم مقاومت کل RT مدار را به شکل زیر محاسبه کنیم:
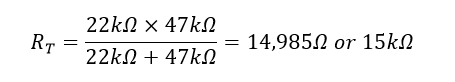
یک نکته مهم که باید در مورد مقاومتهای موازی به خاطر بسپارید، این است که مقاومت کل مدار (RT) دو مقاومت که به طور موازی متصل شدهاند، همواره از مقدار کوچکترین مقاومت در آن ترکیب، کمتر خواهد بود.
در مثال بالا، مقدار مقاومت معادل RT = 15kΩ محاسبه شد، در حالی که مقدار کوچکترین مقاومت 22kΩ است، که بسیار بالاتر میباشد. به عبارت دیگر، مقاومت معادل یک شبکه موازی همیشه از کوچکترین مقاومت در مدار، کمتر خواهد بود.
همچنین، در مواردی که R۱ برابر با مقدار R۲، یعنی R۱ = R۲ باشد، مقاومت کل شبکه دقیقا نصف مقدار یکی از مقاومتها، یعنی R/2 خواهد بود.
به همین ترتیب، اگر سه یا چند مقاومت با مقادیر یکسان به طور موازی به هم متصل شوند، در این صورت مقاومت معادل برابر با R/n خواهد بود، که در آن R مقدار مقاومت و n تعداد مقاومتها در مدار است.
به عنوان مثال، شش مقاومت 100 اهمی در یک ترکیب موازی به یکدیگر متصل شدهاند. بنابراین مقاومت معادل این خواهد بود: RT = R/n = 100/6 = 16.7Ω. اما توجه داشته باشید که این تنها برای مقاومتهایی صادق است که مقادیر یکسان داشته باشند.
جریان در مدار مقاومت موازی
جریان کل IT که وارد مدار مقاومت موازی میشود، مجموع جریانهای منفردی است که در تمام شاخه های موازی جریان دارد. اما مقدار جریان عبوری از هر شاخه موازی ممکن است با دیگری یکسان نباشد، زیرا مقدار مقاومت هر شاخه، میزان جریان عبوری از آن شاخه را تعیین میکند.
به عنوان مثال، اگرچه ولتاژ در هر یک از شاخههای موازی یکسان است، مقاومتها ممکن است متفاوت باشند. پس بر اساس قانون اهم، جریان عبوری از هر مقاومت قطعا متفاوت خواهد بود.
دو مقاومت موازی بالا را در نظر بگیرید. جریانی که از هر یک از مقاومتهای موازی عبور میکند (IR1 و IR2) لزوما یکسان نیست، چراکه به مقدار مقاومت بستگی دارد. با این حال، میدانیم جریانی که در نقطه A وارد مدار شده است، باید از نقطه B خارج شود.
قانون جریان کیرشهف بیان میکند که: «کل جریانی که از مدار خارج میشود برابر با جریان ورودی به آن است – هیچ جریانی از بین نمیرود». بنابراین، کل جریان جاری در مدار به شرح محاسبه میشود:
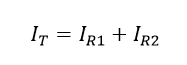
با استفاده از قانون اهم، میتوانیم جریان عبوری از هر مقاومت موازی نشان داده شده در مثال شماره ۲ را به صورت زیر محاسبه کنیم:
جریان عبوری از مقاومت R۱:
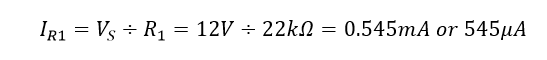
جریان عبوری از مقاومت R۲:
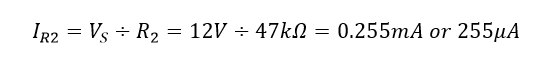
در نتیجه، کل جریان IT عبوری از مدار برابر است با:
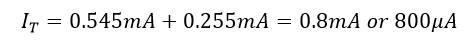
و این مستقیما با استفاده از قانون اهم نیز قابل تایید است:
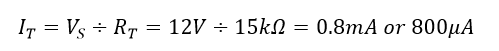
معادلهای که برای محاسبه جریان کل عبوری از یک مدار مقاومت موازی، که مجموع تمام جریانها در شاخههای مختلف است، به شکل زیر به دست میآید:
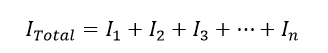
پس میتوان شبکههای مقاومت موازی را به عنوان «تقسیم کننده جریان» در نظر گرفت، زیرا جریان تغذیه بین شاخههای مختلف موازی منشعب یا تقسیم میشود. بنابراین یک مدار مقاومت موازی باتعداد N مقاومت، دارای N مسیر جریان متفاوت است با ولتاژ مشترک است. همچنین میتوان مقاومتهای موازی را بدون تغییر مقاومت کل یا جریان کل مدار با یکدیگر عوض کرد.
مثال ۳
جریان شاخههای جداگانه و جریان کل حاصل از منبع تغذیه را برای مجموعه مقاومتهای زیر، که در یک ترکیب موازی به یکدیگر متصل شدهاند محاسبه کنید.
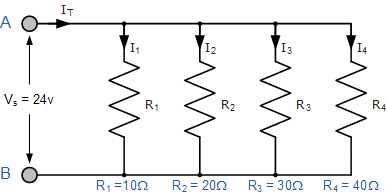
از آنجا که ولتاژ تغذیه در تمام مقاومتهای مدار موازی مشترک است، میتوانیم از قانون اهم برای محاسبه جریان شاخهها به شرح زیر استفاده کنیم.
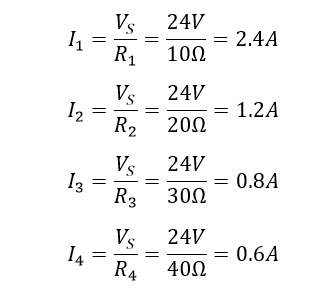
پس جریان کل مدار (IT) که وارد ترکیب موازی مقاومتها میشود، برابر است با:
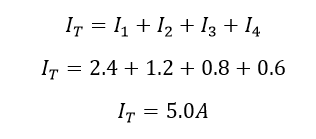
همچنین این مقدار 5 آمپری جریان کل مدار را میتوان با یافتن مقاومت معادل (RT) شاخههای موازی و تقسیم ولتاژ تغذیه (VS) به آن، بررسی و تایید کرد.
مقاومت معادل مدار:
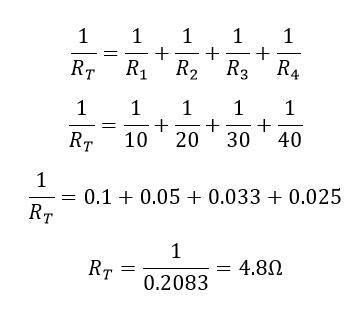
جریان عبوری از مدار برابر است با:
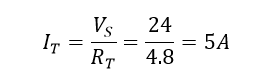
خلاصه اتصال موازی مقاومتها
بنابراین برای جمع بندی: هنگامی که دو یا چند مقاومت به هم متصل شوند، به طوری که هر دو ترمینال آنها به ترتیب به دو ترمینال مقاومتهای دیگر وصل شده باشد، گفته میشود که به صورت موازی به هم متصل شدهاند. ولتاژ دو سر هر مقاومت در یک ترکیب موازی دقیقا یکسان است، اما جریانهایی که از آنها میگذرد یکسان نیستند، چراکه با توجه به مقدار مقاومت آنها و قانون اهم تعیین میشود. پس مدارهای موازی تقسیم کننده جریان هستند.
مقاومت معادل یا کل (RT) یک ترکیب موازی از طریق جمع وارونه مقادیر آنها یافت میشود و مقدار مقاومت کل همواره از کوچکترین مقاومت موجود در ترکیب، کمتر خواهد بود. شبکههای مقاومت موازی را میتوان در همان ترکیب، بدون تغییر مقاومت یا جریان کل مدار، تعویض کرد. مقاومتهایی که در مدار موازی به هم متصل شدهاند، حتی اگر یک مقاومت در مدار باز باشد، به کار خود ادامه میدهند.
تاکنون شبکههای مقاومت را به صورت سری یا موازی مشاهده کردهایم. در آموزش بعدی در مورد مقاومتها، به اتصال هم زمان مقاومتها به صورت ترکیب سری و موازی، و در نتیجه تولید یک مدار مقاومتی ترکیبی، خواهیم پرداخت.
منبع
منبع:ردرونیک