فهرست مطالب
-
مقاومت در مدار AC
-
نمادهای مورد استفاده برای نمایش تغذیه DC و AC
-
رابطه فازی و نمودار برداری V-I
-
شکل موج توان در مدار مقاومتی خالص
-
مثال ۱
-
مثال ۲
مقاومت ها همچنین میتوانند در منابع جریان متناوب استفاده شوند، که در آن برای ولتاژ، جریان و توان مصرفی مقادیر rms داده میشود.
در آموزشهای قبلی مقاومتها و اتصالات آنها را بررسی کرده و از قانون اهم برای محاسبه ولتاژ، جریان و توان آنها استفاده کردهایم. در همه موارد، پلاریته (قطب) و جهت ولتاژ و جریان ثابت فرض شدهاند، به عبارت دیگر جریان مستقیم یا DC.
اما نوع دیگری از تغذیه وجود دارد که به عنوان جریان متناوب یا AC شناخته میشود. در تغذیه AC، پلاریته ولتاژ در طول زمان از مثبت به منفی و بالعکس تغییر میکند و جهت جریان نیز با توجه به ولتاژ، نوسان میکند. شکل نوسانی منبع تغذیه AC از فرم ریاضی یک «موج سینوسی» پیروی میکند و معمولا شکل موج سینوسی نامیده میشود. بنابراین، ولتاژ سینوسی میتواند به عنوان V(t) = Vmax Sin ωt تعریف شود.
هنگام استفاده از مقاومت خالص در مدارهای AC، که دارای مقادیر ناچیز اندوکتانس یا خازنی هستند، همان اصول و قوانین مدار مرتبط با ولتاژ، جریان و توان، از جمله قانون اهم (و حتی قوانین کیرشهف)، همانند مدارهای مقاومتی DC، صادق هستند. تنها تفاوت آن در استفاده از مقادیر آنی «قله به قله» (peak-to-peak) یا «rms» است.
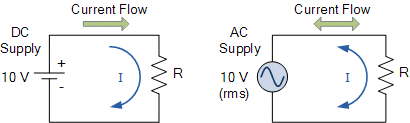
معمولا هنگام کار با ولتاژ و جریان متناوب AC، برای جلوگیری از سردرگمی، تنها از مقادیر «rms» استفاده میشود. مقدار rms یا «جذر میانگین مربع» یک شکل موج AC، مقدار موثر یا مقدار معادل DC برای آن است. همچنین، نماد شماتیک مورد استفاده برای تعریف منبع ولتاژ AC، بر خلاف نماد باتری برای DC، یک خط «موج دار» است که در شکل زیر نشان داده شده است.
نمادهای مورد استفاده برای نمایش تغذیه DC و AC
مقاومتها قطعات «پسیو (غیر فعال)» هستند، یعنی هیچ انرژی الکتریکی تولید یا مصرف نمیکنند، بلکه انرژی الکتریکی را به گرما تبدیل میکنند. در مدارهای DC، مقدار مقاومت، نسبت خطی ولتاژ به جریان آن است. با این حال در مدارهای متناوب، این نسبت ولتاژ به جریان، به فرکانس و اختلاف فاز یا زاویه فاز (φ) منبع بستگی دارد. بنابراین هنگام استفاده از مقاومت در مدارهای AC، معمولا اصطلاح امپدانس با نماد Z مورد استفاده قرار میگیرد و میتوان گفت مقاومت DC برابر است با امپدانس AC. R = Z.
توجه به این نکته مهم است که هنگام استفاده در مدارهای متناوب، بدون توجه به فرکانس منبع، از DC تا فرکانسهای بسیار بالا، یک مقاومت همواره مقدار یکسانی خواهد داشت، برخلاف خازن و سلف.
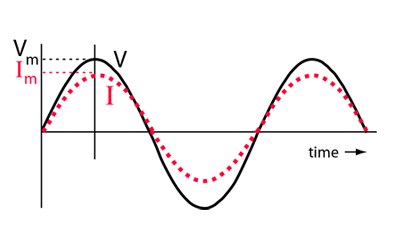
برای مقاومتهای موجود در مدارهای AC، جهت جریان عبوری از آنها تاثیری در رفتار مقاومت ندارد، بنابراین تغییرات ولتاژ، بالا و پایین میرود. جریان و ولتاژ، دقیقا به طور همزمان، به حداکثر رسیده، از صفر میگذرند و به حداقل میرسند. به عبارت دیگر، همان طور که در شکل زیر آمده، آنها همزمان بالا و پایین میروند و گفته میشود که «هم فاز».
رابطه فازی و نمودار برداری V-I
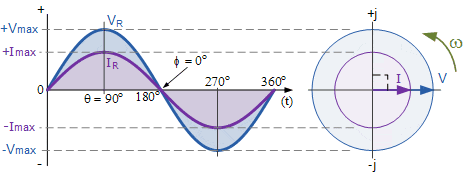
میتوانیم ببینیم که در هر نقطه از محور افقی، ولتاژ و جریان لحظهای هم فاز هستند، زیرا جریان و ولتاژ به طور همزمان به حداکثر مقادیر خود میرسند ، یعنی زاویه فاز (θ) آنها 0° است. پس میتوان به راحتی با استفاده از قانون اهم، این مقادیر لحظهای ولتاژ و جریان را مقایسه کرد و مقدار مقاومت را به دست آورد. مدار شکل زیر، متشکل از منبع AC و مقاومت را در نظر بگیرید.
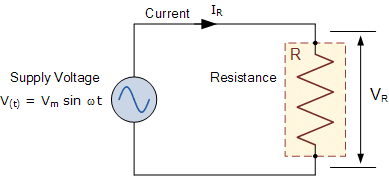
ولتاژ لحظهای دو سر مقاومت (VR) برابر با ولتاژ تغذیه (Vt) است و به صورت زیر ارائه میشود:
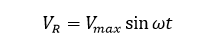
بنابراین، جریان لحظهای مقاومت به این صورت است:
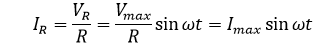
از آنجا که ولتاژ یک مقاومت برابر VR = I.R است، ولتاژ لحظهای دو سر مقاومت نیز میتواند به صورت محاسبه شود:
![]()
در مدارهای سری AC مقاومتی خالص، میتوان تمام افت ولتاژهای دو سر مقاومتها را با هم جمع کرد تا ولتاژ کل مدار را به دست آورد، زیرا تمام ولتاژها با یکدیگر هم فاز هستند. به همین ترتیب، در یک مدار موازی AC مقاومتی خالص، میتوان تمام جریانهای شاخههای مختلف را با هم جمع کرد تا جریان کل را به دست آورد، زیرا تمام جریانهای شاخهها با یکدیگر هم فاز هستند.
از آنجا که برای مقاومت در مدارهای AC، زاویه فاز φ بین ولتاژ و جریان صفر است، ضریب توان مدار برابر cos0° = 1.0 میباشد. توان مدار را در هر لحظه از زمان، با ضرب ولتاژ و جریان در آن لحظه میتوان یافت.
پس توان (P) مصرف شده توسط مدار با واحد وات، به صورت P = VrmsIcosφ محاسبه میشود. اما از آنجا که در یک مدار کاملا مقاومتی cos(φ) = 1 است، بر اساس قانون اهم، توان مصرفی به سادگی P = Vrms I میباشد.
پس این شکل موج «توان» را به ما میدهد که در شکل زیر به صورت یک مجموعه از پالسهای مثبت نشان داده شده است. وقتی ولتاژ و جریان هر دو در نیمه مثبت سیکل (چرخه) قرار دارند، توان حاصل مثبت است و هنگامی که ولتاژ و جریان هر دو منفی باشند، حاصل ضرب دو مقدار منفی یک پالس توان مثبت میدهد.
شکل موج توان در مدار مقاومتی خالص
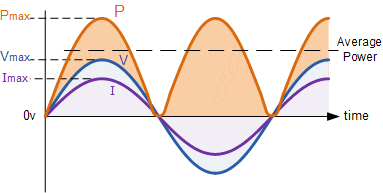
پس توان تلف شده در یک بار کاملا مقاومتی که از منبع AC rms تغذیه میشود، همان توانی است که برای یک مقاومت متصل به منبع تغذیه DC وجود دارد:
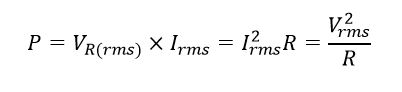
که در آن:
P: توان میانگین با واحد وات،
Vrms: ولتاژ تغذیه rms با واحد ولت،
Irms: جریان تغذیه rms با واحد آمپر و
R: مقدار مقاومت با واحد اهم است – که برای نشان دادن امپدانس، باید با نماد Z نمایش داده شود.
اثر حرارتی تولید شده توسط یک جریان متناوب با حداکثر مقدار Imax با جریان DC با همان مقدار، یکسان نیست. برای مقایسه اثر حرارتی AC با اثر معادل DC، باید از مقادیر rms استفاده شود. هر عنصر گرمایشی مقاومتی مانند بخاری برقی، توستر، کتری، اتو، آب گرم کن و غیره، میتواند به عنوان یک مدار مقاومتی AC طبقه بندی شود، چراکه ما از مقاومت در مدارهای AC برای گرم کردن خانه و آب استفاده میکنیم.
مثال ۱
یک عنصر گرمایشی 1000 وات (1kW) به ولتاژ تغذیه 250V AC متصل است. امپدانس (مقاومت AC) عنصر در هنگام گرم بودن و مقدار جریان گرفته شده از منبع را محاسبه کنید.
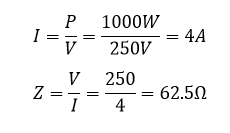
مثال ۲
توان مصرف شده توسط یک عنصر مقاومتی 100Ω متصل به منبع تغذیه 240V را محاسبه کنید.
از آنجا که تنها یک عنصر، مقاومت، به منبع متصل است، پس VR = VS.
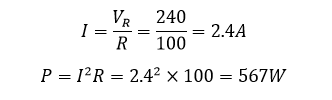
بنابراین برای جمع بندی: در یک مدار AC مقاومتی خالص، گفته میشود جریان و ولتاژ «هم فاز» هستند، زیرا هیچ اختلاف فازی بین آنها وجود ندارد. جریان عبوری از مقاومت رابطه مستقیم با ولتاژ دو سر آن دارد و این رابطه خطی در یک مدار AC امپدانس نامیده میشود. همانند مدارهای DC، هنگام کار با مقاومت در مدارهای AC، میتوان از قانون اهم برای محاسبه ولتاژ، جریان و توان آنها استفاده کرد.
منبع:ردرونیک