انواع اتصالات مداری مقاومت‌‌ها

انواع اتصالات مداری مقاومت‌‌ها – مدارهای سری و موازی مقاومت‌ها

مقاومت‌ها می‌توانند به دو صورت موازی و سری در مدار قرار گیرند. حال می‌خواهیم بررسی کنیم که در هر کدام از این دو حالت، مقادیر جریان، ولتاژ و مقاومت معادل چگونه خواهد بود. در ادامه به برسی بیشتر این مطالب ابتدایی الکترونیک می پردازیم تا شما را به دنیای جذاب الکترونیک وارد کنیم  با ما باشید.

اتصال سری مقاومت‌ها

می‌خواهیم ببینیم که در صورت اتصال تعدادی مقاومت به صورت سری به  یک‌دیگر، چه اتفاقی می‌افتد. فرض می‌کنیم سه مقاومت با اندازه‌های متفاوت داریم.

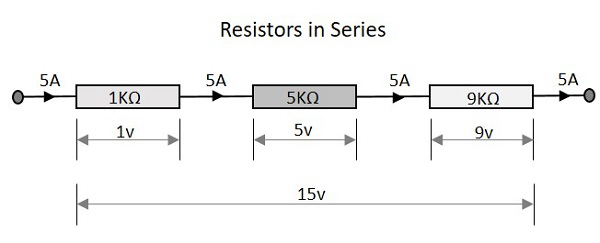
مقاومت معادل

مقاومت معادل مداری که مقاومت‌های آن به صورت سری هستند، برابر با مجموع تک تک آن‌ مقاومت‌ها خواهد بود. یعنی به عنوان مثال در مدار تصویر بالا که سه مقاومت سری با مقادیر 1 KΩ ، 5 KΩ  و 9 KΩ داریم، مطابق این قانون، مقاومت معادل این شاخه از مدار به شکل زیر محاسبه می‌گردد:

R = R₁ + R₂ + R₃

R = R₁ + R₂ + R₃ = 1+5+9 = 15 KΩ

( R₁ مقدار اولین مقاومت، R₂  مقدار دومین مقاومت و R₃ مقدار سومین مقاومت است.)

ولتاژ

ولتاژ کلی دو سر یک شبکه‌ی مقاومتی سری، از مجموع ولتاژ‌های دوسر تک تک مقاومت‌ها بدست می‌آید. به عنوان مثال در مدار تصویر بالا، سه مقاومت سری داریم که دو سر هر کدام مقدار متفاوتی ولتاژ ایجاد شده است. بنابراین ولتاژ معادل دو سر شاخه به این شکل خواهد بود:

V = V₁ + V₂ + V₃

V = V₁ + V₂ + V₃ = 1 v+5 v +9 v= 15 v

(V₁ ولتاژ دو سر مقاومت اولی ، V₂  ولتاژ دو سر مقاومت دومی و V₃ ولتاژ دو سر مقاومت سومی است.)

جریان

مقدار جریان معادلی که از یک شاخه مقاومتی با اتصال سری عبور می‌کند، در تمام نقاط آن شاخه یکسان است. بنابراین در مدار بالا هم، جریان عبوری در نقطه‌ی ورودی شاخه، در نقاط میانی بین مقاومت‌ها و هم‌چنین در نقطه خروجی شاخه، همگی برابر همان 5 آمپر است. به عبارتی در اتصال سری داریم:

I = I₁ = I₂ = I₃

(I₁ جریان عبوری از مقاومت اول ، I₂  جریان عبوری از مقاومت دوم و I₃ جریان عبوری از مقاومت سوم است.)

اتصال موازی مقاومت‌ها

حالا بررسی می‌کنیم اگر تعدادی مقاومت به صورت موازی با یک‌دیگر در مدار اتصال داشته باشند، چه اتفاقی خواهد افتاد. فرض می‌کنیم مانند تصویر زیر، سه مقاومت را به شکل موازی به هم اتصال داده باشیم.

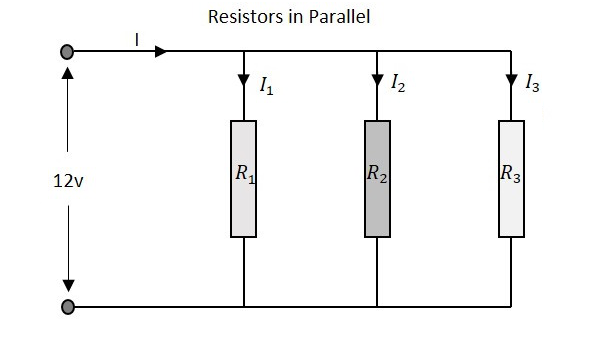
مقاومت معادل

محاسبه‌ی مقاومت معادل در شبکه‌ای که مقاومت‌های آن اتصال موازی دارند، کمی با حالت سری متفاوت است. در اینجا باید ابتدا معکوس مقدار تک تک مقاومت  محاسبه شود و سپس این مقادیر با هم جمع شوند. حاصل این جمع، معکوس جبری مقدار مقاومت معادل خواهد بود.

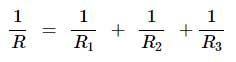
R₁ مقدار اولین مقاومت، R₂  مقدار دومین مقاومت و R₃ مقدار سومین مقاومت در شبکه مثال زده شده در تصویر فوق است. به این ترتیب با فرض اینکه مقادیر مقاومت‌ها به ترتیب برابر 1 KΩ ، 5 KΩ و 9 KΩ است،  مقدار عددی مقاومت معادل را محاسبه می‌کنیم:

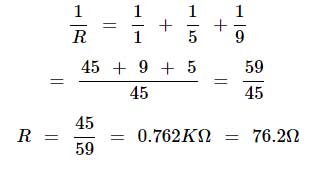
اصلاحیه: مقدار نهایی محاسبه بالا اشتباه است و باید 762Ω می‌شد.

اگر دو مقاومت موازی داشته باشیم می‌توانیم فرمول فوق برای محاسبه مقاومت معادل را به شکل زیر ساده تر کنیم:

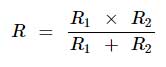
ولتاژ

ولتاژ معادلی که دو سر یک شبکه که دارای مقاومت‌های موازی است می‌افتد برابر با ولتاژ افتاده روی دو سر تک تک مقاومت‌ها است. ( ولتاژ تمام مقاومت ها و ولتاژ معادل همگی با هم برابر است.)  یعنی در مدار فوق داریم:

V = V₁ = V₂ = V₃

(V₁ ولتاژ دو سر مقاومت اولی ، V₂  ولتاژ دو سر مقاومت دومی و V₃ ولتاژ دو سر مقاومت سومی است.)

بنابراین در یک شبکه مقاومتی موازی، ولتاژ در تمام نقاط با هم برابر است.

جریان

جریانی معادلی که به یک شبکه مقاومتی موازی وارد می‌شود، برابر با مجموع جریان‌هایی است که به تک تک شاخه‌های موازی آن شبکه وارد می‌شوند. مقدار جریان هر شاخه را نیز مقدار مقاومت آن تعیین می‌کند. یعنی به عنوان مثال در مدار سه شاخه‌ی فوق داریم:

I = I₁ + I₂ + I₃

که I₁ جریان عبوری از مقاومت اول ، I₂  جریان عبوری از مقاومت دوم و I₃ جریان عبوری از مقاومت سوم است و I نیز معادل جریان کل ورودی به شبکه است.

یکی از کاربردهای رایج مقاومت‌ها در بسیاری از مدار‌ها، قرار گرفتن به عنوان بار خروجی مدار است. اگر هیچگونه بار مقاومتی‌ای برای شبکه وجود نداشته باشد، یک مقاومت را پیش از قسمت بار قرار می‌دهند. مقاومت‌ها یکی از المان‌های ساده در مدار‌ها هستند.

منبع:  میکرودیزاینرالکترونیک