فهرست مطالب
-
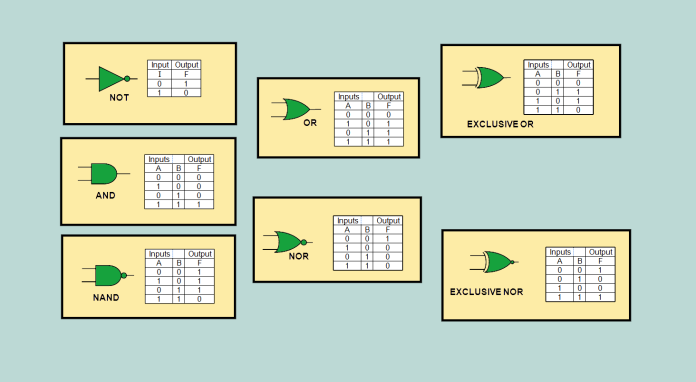
جداول درستی جبر بولی
-
گیت دو ورودی AND
-
گیت دو ورودی OR (OR شاملشدن)
-
گیت NOT (وارونساز)
-
گیت دو ورودی NAND (NOT AND)
-
گیت دو ورودی NOR (NOT OR)
-
گیت دو ورودی Ex-OR (Exclusive OR)
-
گیت دو ورودی Ex-NOR (Exclusive NOR)
-
خلاصهی گیتهای منطقی دو ورودی
از عبارات جبر بولی، میتوان برای ساخت جدول درستی منطق دیجیتال برای توابع مربوطه، استفاده کرد.
علاوه بر یک عبارت بولی استاندارد، اطلاعات ورودی و خروجی هر مدار یا گیت منطقی را میتوان در یک جدول استاندارد رسم کرد؛ تا یک نمایش بصری از عملکرد سوئیچینگ سیستم را ارائه دهد.
جدولی که برای نشاندادن عبارت بولی یک تابع گیت منطقی استفاده میشود؛ معمولا جدول درستی نامیده میشود. جدول درستی گیت منطقی، هر ترکیب ورودی ممکن را از گیت یا مدار خروجی حاصل، بسته به ترکیب ورودی(ها) نشان میدهد.
برای مثال، یک مدار منطقی دو ورودی منحصربفرد را درنظر بگیرید؛ که متغیرهای آن دارای برچسب A و B میباشند. “چهار” ترکیب ورودی ممکن یا ۲۲ حالت “خاموش” و “روشن” برای دو ورودی خواهیم داشت.
با اینحال، هنگام سروکار داشتن با عبارات بولین و مخصوصا جداول درستی گیت منطقی، معمولا اصطلاح”خاموش” یا “روشن” را بهکار نمیبریم؛ بلکه به آنها مقدار بیت را اختصاص میدهیم؛ که سطح منطق “۰” یا منطق “۱” را میتواند بهترتیب اختیار کند.
درنتیجه برای چهار ترکیب ممکن از A و B برای گیت منطقی دو ورودی، خواهیم داشت:
ترکیب ورودی ۱: “خاموش”- “خاموش” یا (۰,۰)
ترکیب ورودی ۲: “خاموش”- “روشن” یا (۰,۱)
ترکیب ورودی ۳: “روشن”- “خاموش” یا (۱,۰)
ترکیب ورودی ۴: “روشن”- “روشن” یا ( ۱,۱)
بنابراین، یک مدار منطقی ۳ ورودی، ۸ یا ۲۳ ترکیب ورودی ممکن و یک مدار منطقی ۴ ورودی، ۱۶ یا ۲۴ ترکیب ورودی ممکن را خواهد داشت و به همین ترتیب، تعداد ورودیها، افزایش مییابد. پس یک مدار منطقی با تعداد “n” ورودی، ۲n ترکیب ورودی ممکن را برای هردو حالت “خاموش” و “روشن” خواهد داشت.
پس بهمنظور ساده نگهداشتن مطالب برای درک کردن، در این آموزش، تنها به گیتهای منطقی استاندارد با دو ورودی، میپردازیم اما قواعد، برای گیتهای با بیشتر از دو ورودی، همچنان یکسان است.
بنابراین، جداول درستی جبر بولی برای یک گیت دو ورودی AND، یک گیت دو ورودی OR و یک گیت تک ورودی NOTبهصورت زیر است:
گیت دو ورودی AND
برای یک گیت دو ورودی AND، خروجی Q، درصورتی که ورودی “A و (AND) B” ،هردو صحیح (true) باشند؛ صحیح (true) است و بهصورت عبارت: (Q=A and B) باید آن را بیان نمود. جدول درستی تابع دو ورودی AND به صورت زیر است.
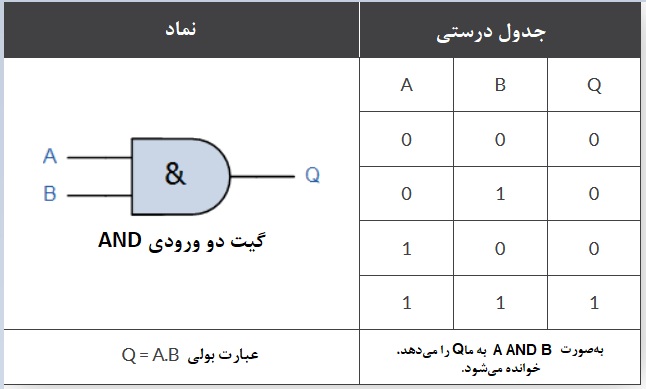
توجه داشته باشید؛ که عبارت بولی برای یک گیت دو ورودی AND، میتواند بهصورت A.B یا بهتنهایی AB بدون نقطه، نوشته شود.
گیت دو ورودی OR (OR شاملشدن)
برای یک گیت دو ورودی OR، خروجی Q درصورتی صحیح (true) است؛ که یکی از ورودی “A یا (OR) B”، صحیح باشد و با عبارت (Q= A OR B) بیان میشود. جدول درستی گیت دو ورودی OR به صورت زیر است.
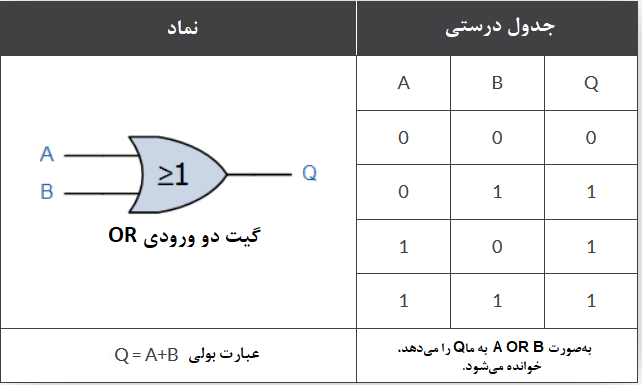
گیت NOT (وارونساز)
برای یک گیت تک ورودی NOT، خروجی Q تنها زمانی صحیح است؛ که ورودی صحیح نباشد (“NOT” true)، به این معنا، که خروجی وارون یا مکمل ورودی است و دارای عبارت بولی (Q= NOT A) میباشد. جدول درستی تابع دو ورودی NOT به صورت زیر است.
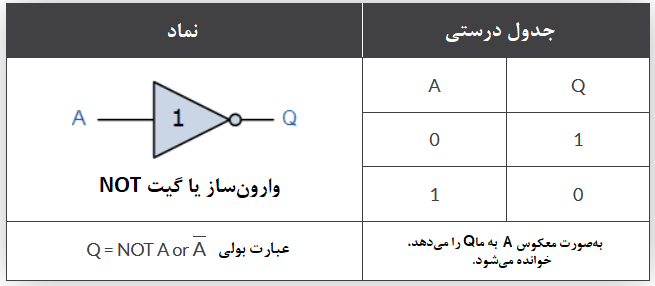
گیتهای NAND و NOR، بهترتیب ترکیبی از گیتهای AND و OR میباشند؛ که دارای گیت NOT(وارونساز) میباشند.
گیت دو ورودی NAND (NOT AND)
برای یک گیت دو ورودی NAND، خروجی Q، درصورتی که هردو ورودی A و B هردو صحیح (true) باشند؛ صحیح نیست (Not true) و بهصورت عبارت: (Q=not(A and B)) باید آن را بیان نمود. جدول درستی تابع دو ورودی NAND به صورت زیر است.
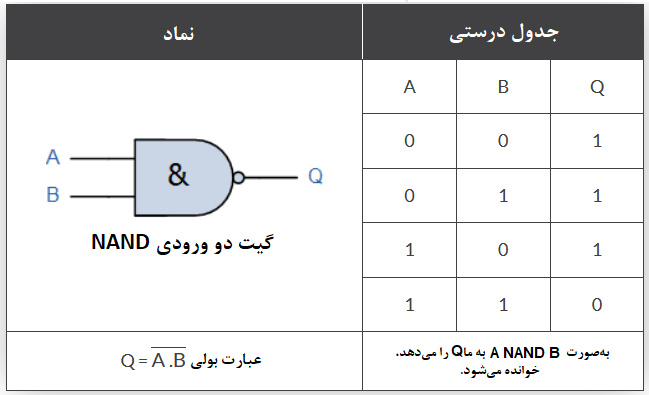
گیت دو ورودی NOR (NOT OR)
برای یک گیت دو ورودی NOR، خروجی Q درصورتی صحیح (true) است؛ که هردو ورودی A و B، صحیح نباشند (Not true) و با عبارت (Q= not(A OR B)) شناخته میشود. جدول درستی تابع دو ورودی NOR به صورت زیر است.
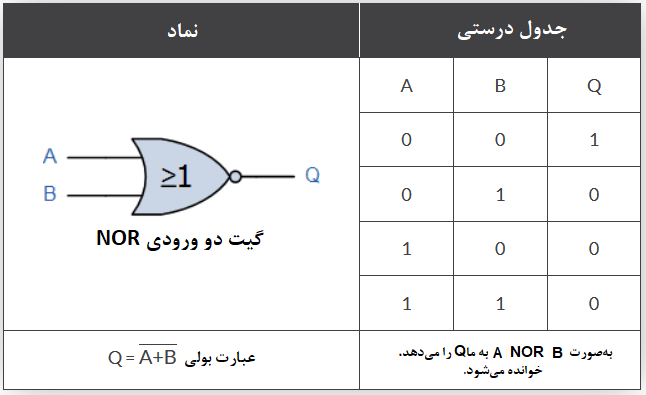
علاوهبر گیتهای استاندارد منطقی، دو نوع خاص از تابع گیت منطقی وجود دارد که بهآنها گیت انحصاری – OR (Exclusive-OR) یا گیت انحصاری – NOR (Exclusive-NOR) گفته میشود. عبارت بولی که نشاندهندهی این دو تابع است؛ با نماد بهعلاوه در یک دایره (⊗) نشان داده میشود.
عملکردهای سوئیچنگ هردوی این نوع گیتها را میتوان با استفاده از گیتهای منطقی استاندارد بالا، ایجاد کرد. اما به دلیل اینکه ایجاد آنها سبب استفاده از توابع زیادی میشود؛ این گیتها به شکل IC استاندارد در دسترس میباشند و دراینجا بهعنوان مرجع گنجانده شدهاند.
گیت دو ورودی Ex-OR (Exclusive OR)
برای یک گیت دو ورودی Ex-OR، خروجی Q درصورتی صحیح است؛ که یکی از دو ورودی A یا B صحیح باشد؛ اما هردو نمیتوانند باهم صحیح باشند. عبارت بولی برای بیان این توضیح Q=(A and NOT B) or (NOT A and B) است. جدول درستی تابع دو ورودی Ex-OR به صورت زیر است.
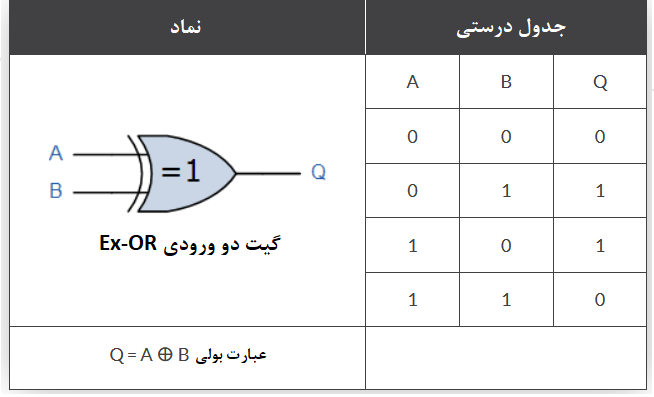
گیت دو ورودی Ex-NOR (Exclusive NOR)
برای یک گیت دو ورودی Ex-NOR، خروجی Q درصورتی صحیح است؛ که هر دو ورودی A یا B برابر باشند یعنی هردو صحیح یا غلط باشند. عبارت بولی برای بیان این توضیح Q=(A and B) or (NOT A and NOT B) است. جدول درستی گیت دو ورودی Ex-NOR به صورت زیر است.
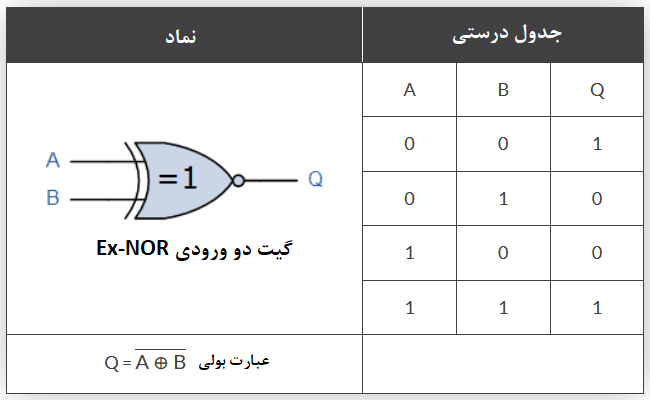
خلاصهی گیتهای منطقی دو ورودی
جدول درستی زیر، توابع منطقی با گیتهای دارای دو ورودی در بالا را باهم مقایسه میکند.
ورودیها |
خروجیهای جدول درستی برای هر گیت |
||||||
B |
A |
AND |
NAND |
OR |
NOR |
Ex-OR |
Ex-NOR |
| ۰ | ۰ | ۰ | ۱ | ۰ | ۱ | ۰ | ۱ |
| ۱ | ۰ | ۰ | ۱ | ۱ | ۰ | ۱ | ۰ |
| ۰ | ۱ | ۰ | ۱ | ۱ | ۰ | ۱ | ۰ |
| ۱ | ۱ | ۱ | ۰ | ۱ | ۰ | ۰ | ۱ |
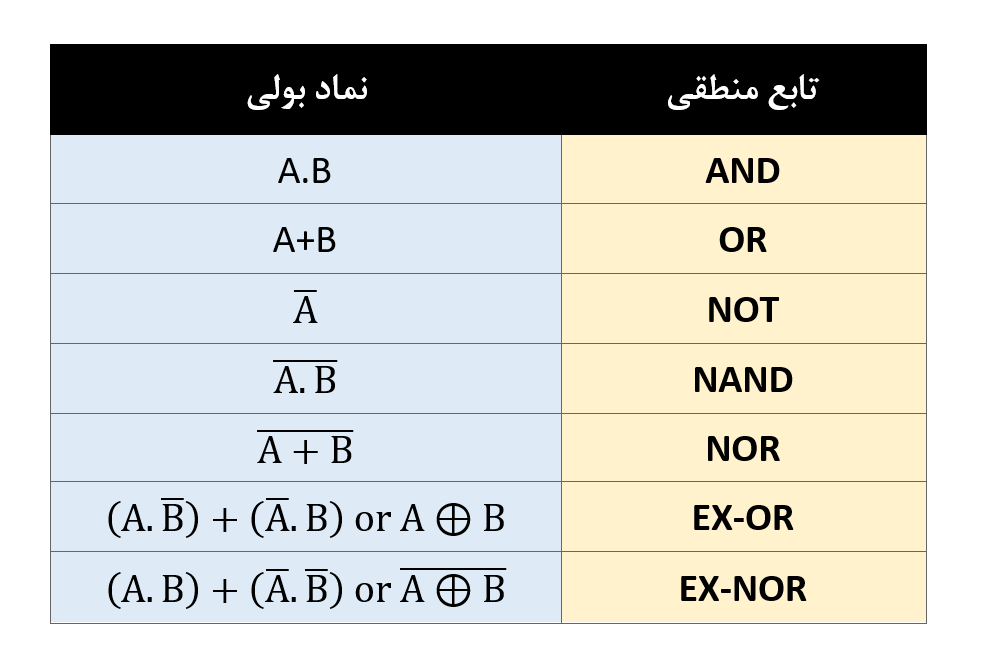
جدول زیر، لیستی از توابع منطقی معروف و نماد معادل بولی آنها را در اختیار ما قرار میدهد.
جداول درستی جبر بولی گیتهای منطقی با دو ورودی، در این آموزش بهعنوان مثالی برای عملکرد تابع گیت منطقی آورده شدند؛ اما گیتهای منطقی بسیار بیشتری با 4،3 و حتی 8 ورودی وجود دارند. گیتهای ورودی چندگانه با گیتهای دو ورودی ساده بالا، تفاوتی ندارد. پس یک گیت AND با چهار ورودی، برای تولید خروجی موردنیاز در Q، به همهی چهار ورودی خود نیاز دارد و درنتیجه دارای جداول درستی جبر بولی بزرگتری خواهدبود.