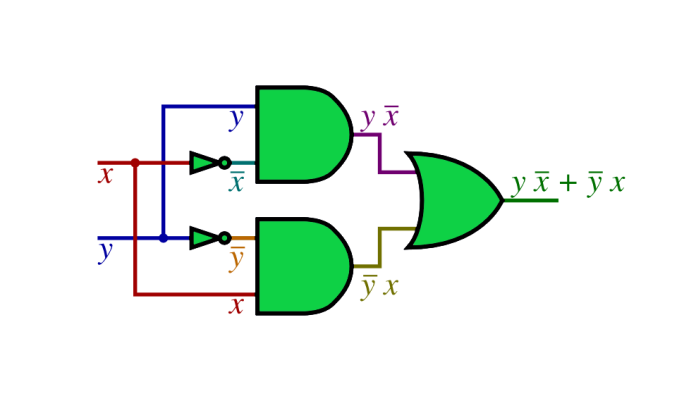
مثالهای جبر بولی، در ارتباط با چگونگی کاهش تعداد گیتهای دیجیتال با استفاده از قوانین جبری است.
جبر بولی و قواعد آن، میتوانند برای شناسایی گیتهای منطقی غیرضروری در طراحی منطق دیجیتال استفاده گردند و از این طریق، میتوان تعداد گیتهای موردنیاز را کاهش داد و در مصرف توان و هزینه، صرفهجویی نمود.
ما در سرتاسر این بخش مشاهده کردیم؛ که توابع منطقی دیجیتال را میتوان بهصورت یک عبارت جبر بولی یا یک جدول درستی گیت منطقی تعریف کرد و نمایش داد. از اینرو، در این آموزش، چند مثال از نحوهی استفاده از جبر بولی برای سادهکردن مدارهای منطقی دیجیتال، آورده شدهاست.
مثال شماره یک جبر بولی
یک جدول درستی برای توابع منطقی در نقاط C، D و Q در مدار زیر بسازید و یک گیت منطقی واحد را شناسایی نمایید؛ که میتواند برای جایگزینی کل مدار، استفاده گردد.
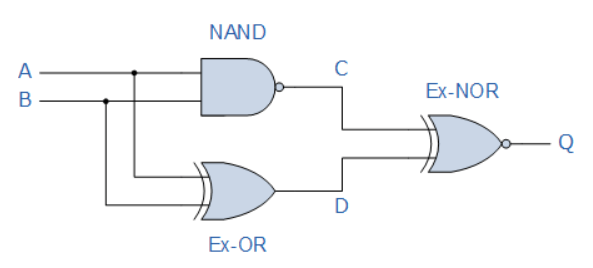
در نگاه اول، مشاهده میکنیم؛ که مدار از یک گیت دو ورودی NAND، یک گیت Ex-OR و درنهایت یک گیت دو ورودی Ex-NOR در خروجی، تشکیل شدهاست. از آنجاییکه، تنها دو ورودی با برچسبهای A و B در مدار وجود دارند؛ 4 ترکیب برای ورودی (2۲) امکانپذیر است و این ترکیبها ۰-۰، ۱-۰،۰-۱ و در آخر ۱-۱ میباشند. رسم توابع منطقی از گیت در قالب جدول، جدول درستی زیر را برای کل مدار منطقی در اختیار ما قرار میدهد.
ورودیها |
خروجی در |
|||
B |
A |
C |
D |
Q |
| ۰ | ۰ | ۱ | ۰ | ۰ |
| ۱ | ۰ | ۱ | ۱ | ۱ |
| ۰ | ۱ | ۱ | ۱ | ۱ |
| ۱ | ۱ | ۰ | ۰ | ۱ |
با استفاده از جدول درستی بالا، ستون C، نشاندهندهی تابع خروجی تولیدشده توسط گیت NAND است؛ درحالیکه، ستون D، تابع خروجی تولیدشده توسط گیت Ex-OR را نشان میدهد. هردوی این عبارات خروجی، به شرط ورودی برای گیت Ex-NOR که در خروجی قرار دارد؛ تبدیل میشوند.
از جدول درستی بالا میبینیم؛ که خروجی در Q زمانی وجود دارد؛ که یکی از دو ورودی A و B در منطق 1 باشند. تنها جدول درستی که با این شرایط تطابق دارد؛ گیت OR است. بنابراین، تمام مدار بالا را میتوان با یک گیت دو ورودی OR جایگزین کرد.
مثال شماره دو جبر بولی
عبارت جبر بولی برای سیستم زیر را بیابید.
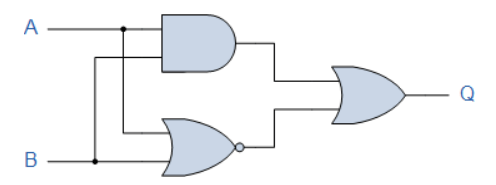
این سیستم، متشکل از یک گیت AND ، یک گیت NOR و درنهایت یک گیت OR میباشد. تابع بکار رفته برای گیت AND، A.B و برای گیت NOR، است. هردوی این عبارات، بهصورت جداگانه، ورودیهای گیت OR میباشند که بهصورت (A+B) تعریف میشود. درنتیجه، عبارت خروجی نهایی بهصورت زیر خواهدبود:
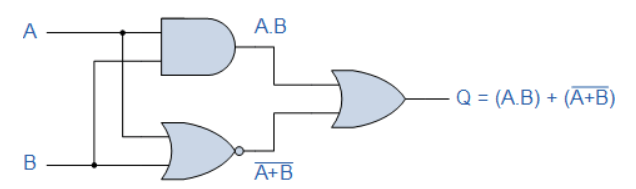
از طرفی با توجه آموزشهای قبل:
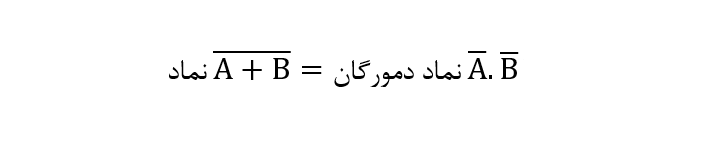
بنابراین نماد خروجی نهایی بهصورت زیر خواهد بود:
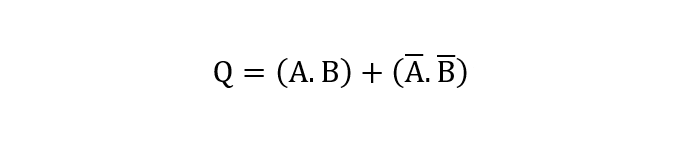
ورودیها |
واسطهها |
خروجی |
||
B |
A |
A.B |
(A+‾B‾) |
Q |
| ۰ | ۰ | ۰ | ۱ | ۱ |
| ۱ | ۰ | ۰ | ۰ | ۰ |
| ۰ | ۱ | ۰ | ۰ | ۰ |
| ۱ | ۱ | ۱ | ۰ | ۱ |
پس، کل مدار بالا را میتوان با یک گیت انحصاری-NOR تنها، جایگزین کرد؛ که در واقع گیت Exclusive-NOR ،خود از این توابع گیتی منحصربفرد ساخته شدهاست.
مثال شماره سه جبر بولی
عبارت جبر بولی برای سیستم زیر را بیابید.
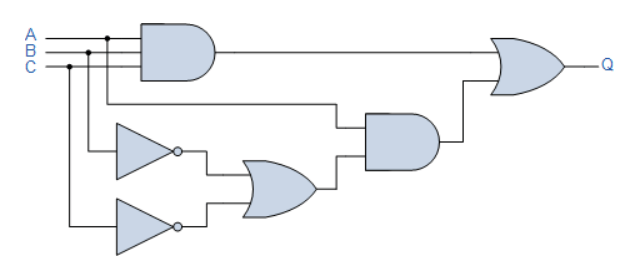
این سیستم ممکن است؛ پیچیدهتر از دو آنالیز قبلی به نظر رسد؛ اما دوباره این مدار منطقی نیز از گیتهای سادهی AND، OR و NOT تشکیل میشود؛ که بههم اتصال یافتهاند.
همانند مثالهای قبلی بولی، میتوان مدار را با نوشتن نمادهای بولی برای هر تابع گیت منطقی، سادهسازی کرد؛ تا عبارت نهایی را، برای خروجی در Q در اختیار ما بگذارد.
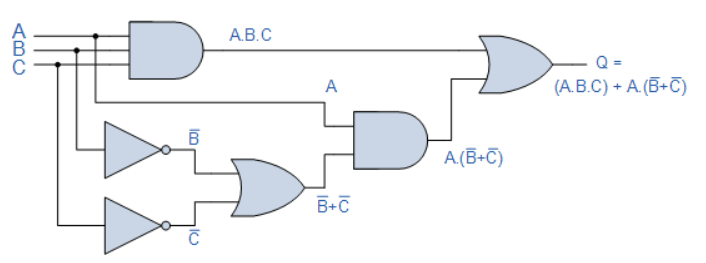
خروجی گیت AND با سه ورودی، تنها زمانی در منطق “1” است؛ که تمام ورودیهای گیت، در حالت بالا (HIGH) و در سطح منطق “1”(A.B.C) باشند. خروجی گیت OR پایینی، تنها زمانی در منطق “1” است؛ که یک یا هردو ورودی B و C، در سطح منطق “0”باشند. “1” شدن برای خروجی گیت ورودی AND زمانی رقم میخورد؛ که ورودی A، برابر با منطق “1” یا ورودیهای B و C، در منطق “0” باشند.
پس خروجی در Q ، در یک حالت برابر با “1” بوده و آن زمانی است؛ که ورودیهای A.B.C برابر با “1” یا A برابر با “1” و هردو ورودی B و C برابر با “0” یعنی:
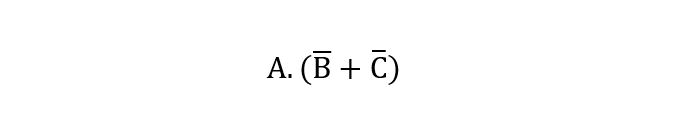
با استفاده از “قضیهی دمورگان“، ورودیهای B و C خنثی میشوند تا یک خروجی را در Q تولید نمایند؛ که میتواند در منطق “1” یا منطق “0” باشد. این امر سبب میشود که ورودی A، تنها ورودی موردنیاز برای نمایش خروجی در Q باشد؛ که در جدول زیر نشان داده شدهاست.
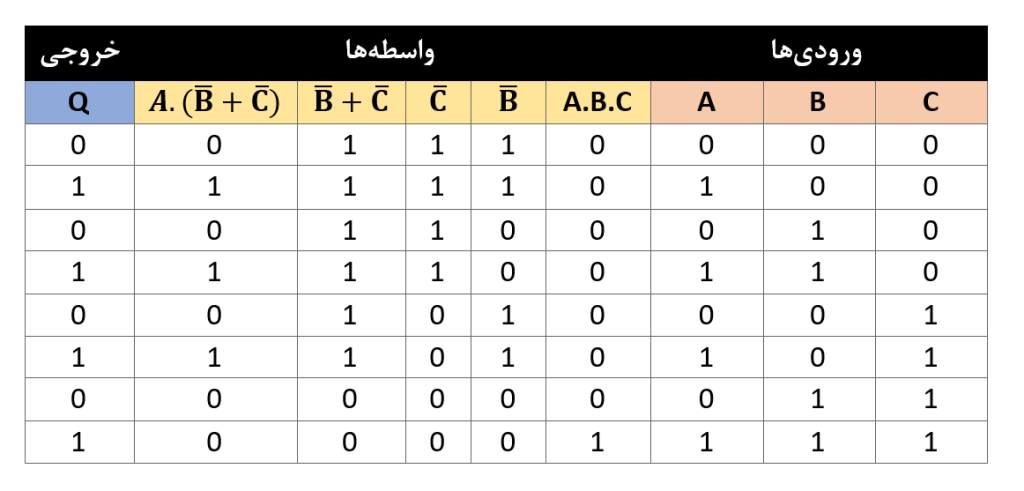
بنابراین، میتوانیم ببینیم؛ که کل مدار بالا را میتوان با یک ورودی تک که با نام “A” برچسبگذاری شدهاست؛ جایگزین نمود و درنتیجه، مداری متشکل از 6 گیت منطقی منفرد را به تنها یک تکه سیم (یا بافر) تقلیل داد. این نوع آنالیز مدار با استفاده از جبر بولی، میتواند بسیار قدرتمند باشد و بهسرعت هر گیت منطقی غیرضروری را در یک طراحی منطق دیجیتال شناسایی کند؛ که سبب کاهش تعداد گیتهای موردنیاز، توان مصرفی مدار و البته هزینه میشود.
منبع
منبع: ردرونیک