فهرست مطالب
-
تئوری سوئیچینگ
-
قضیهی سوئچینگ یک کلید
-
قضیهی سوئیچینگ یک کلید معمولا- باز(Normally-open)
-
جدول درستی سوییچینگ
-
قضیهی سوئیچینگ کلیدهای سری
-
قضیهی سوئیچینگ کلیدهای سری
-
جدول درستی کلید سری
-
گیت منطقی AND دیجیتال
-
قضیهی سوئیچینگ کلیدهای موازی
-
جدول درستی کلید موازی
-
گیت منطقی OR دیجیتال
-
قضیهی سوئیچینگ تابع بولی
-
قانون همانی کلیدها
-
قانون همانی تابع AND
-
قانون همانی تابع OR
قضیهی سوئچینگ یک کلید
ممکن است شما تصورداشته باشید؛ که منظور از سوئیچ، کلیدی است که میتواند برای “روشن” یا “خاموش” کردن یک بار نوری (lighting bar) استفاده شود؛ اما یک کلید، همچنین میتواند یک عنصر مکانیکی یا الکترومکانیکی پیچیده باشد؛ که برای کنترل جریان از طریق آن، در هر جهتی میتواند مورد استفاده قرار گیرد و این امر، آن را به یک دستگاه دو طرفه تبدیل میکند. مدار نشان دادهشده در شکل زیر را درنظر بگیرید.
قضیهی سوئیچینگ یک کلید معمولا- باز(Normally-open)
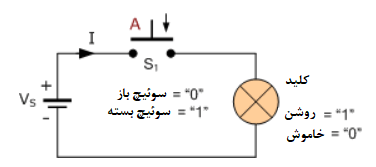
در این مثال ساده، لامپ (L) به منبع باتری (Vs) از طریق یک کلید معمولا-باز (S۱)، متصل میشود. بنابراین، اگر کلیدS۱ زده نشود و باز بماند؛ هیچ جریانی (I) در لامپ شارش نمییابد و درنتیجه “خاموش” مانده و روشن نمیشود. به همین ترتیب، اگر کلید S۱ بسته شود؛ شارش جریان در مدار انجام گرفته و لامپ (L)، “روشن” شده و نور میتاباند. در شرایط معمولی حالت پایدار سوئیچ، معمولا- باز (Normally-open) بوده و بنابراین، لامپ، “خاموش” است.
ما میتوانیم از جبر سوئیچینگ برای توصیف عملکرد یک مدار شامل یک کلید S۱ استفاده کنیم. برای مثال، اگر به یک کلید معمولا-باز، برچسب متغیر “A” را بزنیم، پس زمانیکه این کلید باز است، این کلید “A” فشرده نشدهاست و میتوانیم ارزش آن را “0” درنظر بگیریم. اما زمانیکه، کلید بسته است، کلید “A” فشرده شدهاست و ارزش آن برابر با “1” خواهد بود. این تئوری جبر سوئیچینگ، برای تمام پیکربندیهای کلید معمولا-باز، صحیح است.
جدول درستی سوییچینگ
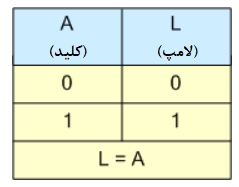
ما میتوانیم این ایدهی نظریهی سوئیچینگ را، با بیان اینکه لامپ، زمانی “روشن” (درحال تابیدن) است؛ که متغیر جبر سوئیچینگ برابر با “۱” باشد و زمانی لامپ “خاموش” (نمیتابد) است؛ که این متغیر برابر با “۰” باشد؛ توسعه دهیم.
به این ترتیب، هنگامیکه، کلید زدهشود (فعال شود)، لامپ “روشن” شده و بنابراین، “A”=1 و “L”=1 است و هنگامیکه، کلید فشرده نشود (فعال نشود)، لامپ “خاموش” مانده و بنابراین، “A”=0 و “L”=0 است. از اینرو، بهدرستی میتوانیم بیان کنیم؛ که برای تئوری سوئیچینگ لامپ، L=A است؛ همانگونه که در جدول درستی، نشان داده شدهاست.
این نوع سوئیچ که در مثال بالا، استفاده شدهاست؛ کلید معمولا-باز (normally-open) و کلید تماسی (make-contact) نامیده میشود؛ زیرا باید بهصورت فیزیکی آن را لمس نمود تا بسته فرض شود (A=1). اما نوع دیگری از چیدمان سوئیچ وجود دارد؛ که کاملا دارای عملکردی برعکس کلید بالا است و کلید معمولا بسته (normally-close) و قطع تماس (break-contact) نامیده میشود؛ زیرا دائما بسته است.
قضیهی سوئیچینگ کلیدهای سری
ما در بالا دیدیم؛ که لامپ (L) را میتوان با استفاده از یک تک سوئیچ S۱، کنترل کرد و زمانیکه، این تک سوئیچ S۱ بسته است (فشرده شدهاست)؛ شارش جریان در مدار برقرار است و لامپ، “روشن” است. اما زمانیکه، ما یک کلید دیگر را بهصورت سری به S۱ متصل نماییم؛ چه تاثیری بر سوئیچینگ مدار و روشنایی لامپ خواهد داشت؟
قضیهی سوئیچینگ کلیدهای سری
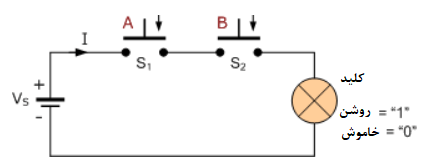
این مدار سوئیچینگ، شامل دو کلید سری با منبع ولتاژ Vs و لامپ میباشد. برای آنکه عملکرد هر سوئیچ منحصربفرد را از هم تشخیص دهیم؛ S۱ را با حرف “A” و S۲ را با حرف “B” برچسبگذاری میکنیم. پس، زمانیکه، هرکدام از کلیدها باز باشند؛ یعنی فشرده نشده اند و میتوانیم ارزش “A” را با “0” و ارزش “B” را نیز با “0” تعریف کنیم.
به همینترتیب، اگر هرکدام از کلیدها بسته یا فشرده شوند؛ میتوانیم ارزش “A” را با “1” و ارزش “B” را نیز با “1” تعریف کنیم. سطح منطق “1”، مرتبط با مقدار ولتاژ منبع تغذیه است و درنتیجه، مثبت است؛ درحالیکه، سطح منطق “1”، مربوط به مقدار ولتاژ صفر یا زمین است.
از آنجاییکه، دو کلید S۱ و S۲ یا”A” و “B” وجود دارند؛ پس چهار ترکیببندی ممکن برای متغیرهای بولی “A” و “B” برای روشنکردن لامپ وجود دارد؛ یعنی “A” باز و “B” بسته باشد، یا “A” بسته و “B” باز باشد یا هردو کلید “A” و “B” همزمان باز یا بسته باشند. برای تعریف این عملکردها جدول درستی زیر را برای نظریهی سوئیچینگ درنظر میگیریم.
جدول درستی کلید سری
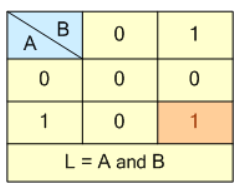
این جدول درستی، نشان میدهد؛ که لامپ تنها در حالتی “روشن” است و میتابد؛ که هردو سوئیچ یعنی کلید A و (AND) کلید B فشرده و بسته شدهباشند. فشردن تنها یک سوئیچ بهتنهایی سبب شارش جریان در مدار نمیشود.
این امر، اثبات میکند؛ که دو کلید S۱ و S۲ بهصورت سری بههم متصل شدهاند و تنها شرط برای شارش جریان (I) و روشنشدن لامپ این است، که هردو بسته باشند. عبارت بولی چنین اتصالی L= A AND B است.
در ترمهای جبر بولی، این عبارت که بیانگر تابع AND است؛ که با یک تک نقطه (.) بین دو متغیر بهصورت L=A.B نشان داده میشود.
بنابراین، هنگامیکه، سوئیچهای بهصورت سری بههم متصل شدهاند؛ تئوری سوئیچینگ و عملکرد مربوطه برابر با گیت منطقی دیجیتالی “AND” است؛ زیرا هردو ورودی باید “1” باشند تا خروجی “1” باشد و در غیراینصورت، خروجی “0” است؛ همانگونه که در تصویر زیر آورده شدهاست.
گیت منطقی AND دیجیتال
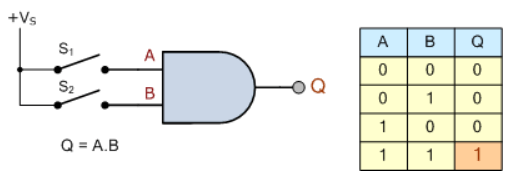
پس اگر ورودی “A” با ورودی “B”، AND شود؛ خروجی “Q” را تولید میکند. در اصطلاحات سوئیچینگ، به تابع AND، تابع حاصلضرب جبر بولی، گفته میشوند.
قضیهی سوئیچینگ کلیدهای موازی
حال، اگر دو کلید S۱ و S۲ را بهصورت موازی همانند شکل زیر بههم متصل کنیم؛ این نوع آرایش، چه تاثیری بر عملکرد سوئیچینگ مدار و روشنایی لامپ خواهد داشت؟
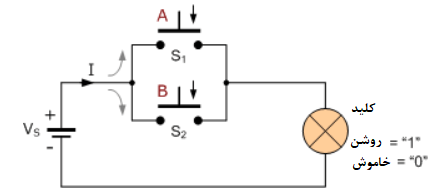
این مدار سوئیچینگ، شامل دو کلید موازی با منبع ولتاژ Vs و لامپ است. همانند قبل، اگر یکی از سوئیچها باز باشد؛ یعنی فشرده نشدهباشد؛ میتوانیم ارزش “A” را با “0” و ارزش “B” را نیز با “0” تعریف کنیم. به همینترتیب، اگر یکی از کلیدها بسته یا فشرده شوند؛ میتوانیم ارزش “A” را با “1” یا ارزش “B” را با “1” تعریف کنیم.
دوباره همانند قبل، با دو کلید S۱ و S۲ یا”A” و “B” ،چهار ترکیببندی ممکن برای متغیرهای بولی “A” و “B” نیاز است؛ تا لامپ روشنایی داشته باشد. این حالتها شامل: “A” باز و “B” بسته باشد، یا “A” بسته و “B” باز باشد یا هردو کلید “A” و “B” همزمان باز یا بسته باشند؛ است. پس، این عملکردهای سوئیچینگ را میتوانیم توسط جدول درستی زیر، تعریف کنیم.
جدول درستی کلید موازی
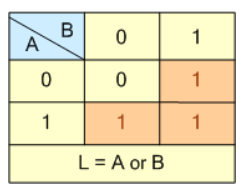
این جدول درستی، نشان میدهد؛ که لامپ، تنها زمانی “روشن” است و میتابد؛ که یکی از دو سوئیچ یعنی کلید A یا (OR) کلید B فشرده و بسته شدهباشند. فشردن هر یک از کلیدها سبب شارش جریان میشود؛ زیرا همیشه یک مسیر هدایت برای لامپ از طریق هر کلید بسته، وجود دارد.بنابراین، این امر، اثبات میکند؛ که دو کلید S۱ و S۲ بهصورت موازی بههم متصل شدهاند و شرط لازم برای شارش جریان (I) و روشنشدن لامپ این است؛ که یکی از دو کلید یا هردو، بسته باشند. عبارت بولی چنین اتصالی L= A OR B است.
در ترمهای جبر بولی، این عبارت که بیانگر تابع OR است؛ که با علامت مثبت یا بهعلاوه (+) بین دو متغیر بهصورت L=A+B نشان داده میشود.
بنابراین، هنگامیکه، سوئیچها بهصورت موازی بههم متصل شدهاند؛ تئوری سوئیچینگ و عملکرد مربوطه برابر با گیت منطقی دیجیتالی “OR” است؛ زیرا اگر دو ورودی باید “0” باشند؛ خروجی “0” باشد و در غیراینصورت، خروجی “1” است؛ همانگونه که در تصویر زیر آورده شدهاست.
گیت منطقی OR دیجیتال
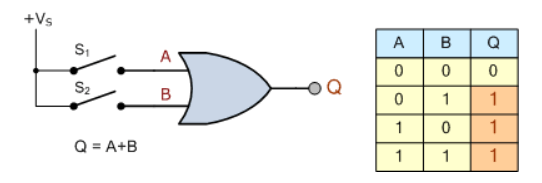
پس اگر ورودی “A” با ورودی “B”، OR شود؛ خروجی “Q” را تولید میکند. در اصطلاحات سوئیچینگ، تابع OR، تابع جمع جبر بولی، نامیده میشود.
قضیهی سوئیچینگ تابع بولی
تئوری سوئیچینگ، میتواند برای پیادهسازی عبارات بولی و همچنین گیتهای منطقی، دیجیتال، استفاده شود. در بالا دیدیم؛ که در ترمهای اتصال کلید، عبارت بولی که از نقطه (.) استفاده میکند؛ بهعنوان اتصال سری برای ضرب بولی تفسیر میشود؛ درحالیکه، عبارت بولی که علامت جمع (+) را بهکار میبرد؛ تفسیرکنندهی اتصال موازی برای جمع بولی است.
مثال شماره ۱ قضیهی سوئیچینگ
تابع بولی Q=A(B+C) زیر را با استفاده از کلیدهایی که روشنکنندهی یک لامپ یا الایدی (LED) میباشند؛ پیادهسازی کنید. همچنین مدار منطقی دیجیتال معادل آن را نیز، نشان دهید.
پیادهسازی کلید
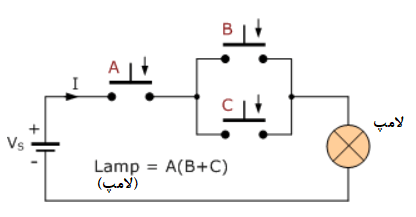
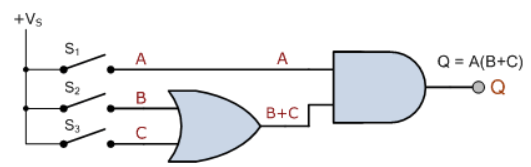
پیادهسازی گیت منطقی
قانون همانی کلیدها
تا اینجا مشاهده کردیم؛ که اتصال کلیدها بهصورت سری یا موازی به یکدیگر، چگونه باعث روشنشدن یک لامپ میشود. اما اگر هردو کلید نشاندهندهی یک تابع بولی AND یا یک تابع OR (عملکردهای ضرب و جمع) از یک تک متغیر بولی A باشند؛ چه خواهد شد؟! در جبر بولی، قوانین و قضیههای مختلفی وجود دارد؛ که میتوان از آنها برای تعریف ریاضیاتی مدارهای منطقی استفاده نمود. یکی از این قضیهها، با نام قانون همانی (idempotent law) شناخته میشود.
قوانین همانی مورداستفاده در تئوری سوئیچینگ، بیان میکنند؛ که AND کردن یا OR کردن یک متغیر با خودش، همان متغیر اولیه و اصلی را تولید میکند. برای مثال، اگر متغیر “A” بامتغیر “A”، AND شود؛ “A” را تولید میکند و به همین ترتیب، اگر متغیر “A” با متغیر “A”، OR شود؛ نتیجه تولید “A” خواهدبود و درنتیجه سادهسازی مدارهای سوئیچ مجاز است و میتوانیم آنها را بهصورت زیر، رسم کنیم.
قانون همانی تابع AND
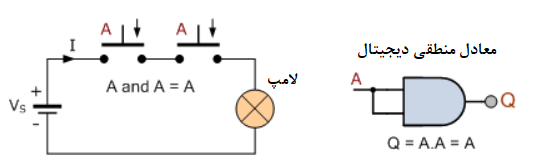
قانون همانی تابع OR
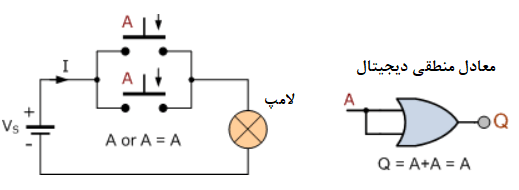
ما در اینجا و در این آموزش دیدیم؛ که روشهای تئوری سوئیچینگ را میتوان برای تحقق عبارات بولی و مدارهای گیت منطقی دیجیتال با استفاده از سوئیچهای ساده “ON/OFF” استفاده کرد.
نمایش توابع “AND“ و “OR” با استفاده از کلیدهای معمولا باز، هم برای ساختن و هم برای درککردن ساده است و نیز بلوکهای ساختمان اصلی بیشتر مدارهای ترکیبی دیجیتال را شکل میدهد.
بنابراین، هر عبارت بولی یا تابع منطقی که داشته باشیم؛ استفاده از تئوری سوئیچینگ برای پیادهسازی آن امکانپذیر است. زیرا، طراحی منطقی، دربارهی استفاده از کلیدها و قطعات الکترومکانیکی، مانند رلههاست.
منبع
منبع:ردرونیک





