عبارت الگوریتم MinMax در انتهای قسمت قبلی آموزش پیادهسازی هوش مصنوعی شطرنج بیان کردیم که البته مدت زیادی هم از انتشار آن میگذرد به تاریخچه پیادهسازی هوش مصنوعی شطرنج پرداختیم و دیدیم که سابقه این ایده حتی به قبل از اختراع کامپیوترهای الکترونیکی برمیگرده که در نوع خودش خیلی هم جذاب میشود. اما مسئلهای که گیجکننده است این است که این منطق دقیقاً چطور عمل میکند، اگر منطق عملکردی به این میزان میتواند ساده باشد که در یک سیستم مکانیکی قابل پیادهسازی است پس چرا اینقدر به نظر پیچیده و درهمتنیده میآید. در این قسمت سعی خواهیم کرد که به شکل کلی جواب این سؤال را بدهیم. جزئیات خیلی زیاد هستند و پرداختن به همه جنبهها قطعاً هم از حوصله این پست و هم از حوصله من خارجه و سعی میکنم با نشاندادن مسیر کلی این ابهام رو از منطق پشت هوش مصنوعی رفع کنم. با ما در ادامه همراه باشید.
هوش مصنوعی شطرنج چطور فکر میکند
سؤال در نگاه اول سخت به نظر میرسد ولی جواب ساده است، هوش مصنوعی شطرنج فکر نمیکند، بله بر خلاف چیزی که از عبارت فوق برداشت میشود اتفاقی که در پشت پرده این الگوریتم میافتد فکرکردن نیست! (البته شاید هم در نگاهی باشد، نمیخواهم وارد بحثهای فلسفی علم انسانی بشوم). پس چه اتفاقی میافتد؟
در واقع ما بهعنوان برنامهنویس دو انتخاب پیش نداریم، راه اول این است که به شکل الگوریتم تمام حالتهای ممکن را برنامهنویسی کنیم به شکل شرطهای تودرتو، همان چیزی که در ساخت دستگاه KRK اتفاق افتاده است. (در قسمت اول مقاله هم فیلم آن را قرار دادیم و هم در خصوص آن توضیح دادیم.)

در آن مورد خاص میشود از این روش استفاده کرد چرا که تعداد حالتهای ممکن بسیار محدود است و شاید پیادهسازی آن کار دشواری نباشد ولی وقتی حرف از بازی شطرنج میشود صحبت از میلیونها میلیون حالت ممکن است که پیادهسازی آن به این شکل قطعاً نشدنی است.
و راه دوم این است که به نحوی هر حرکت را امتیازدهی کنیم و در حرکتهای ممکن امتیازهای کسب شده را بررسی کنیم، در نهایت آن حرکتی را انجام دهیم که بالاترین امتیاز را کسب کرده است. این قاعده به الگوریتم minmax مشهور است و برای بازیکردن اغلب بازیهای کامپیوتری از همین روش استفاده میشود (تا قبل از این که هوش مصنوعی وارد عرصه شود) در ادامه جزئیات بیشتری از الگوریتم را بررسی خواهیم کرد.
الگوریتم MinMax چیست
در واقع این الگوریتم مکانیسمی نزدیک منطق تصمیمگیری ما دارد، این الگوریتم سعی میکند با کمترین هزینه (مینیمم) تصمیمی بگیرد که بیشترین سود (ماکزیمم) را نصیب ما کند. با فرض این که حریف به شکل منطقی بازی کند از این الگوریتم میتوان دربازیهای دونفره نوبتی به شکل گسترده استفاده کرد. دربازیهای مثل بازی دوز (Tic-Tac-Toe) یا منطق شطرنج یا تخته نرد و امثالهم.
در الگوریتم minmax به دو بازیکن حداکثرکننده و حداقلکننده گفته میشود، حداکثر کننده سعی میکند که بالاترین امتیاز ممکن را بگیرد و در مقابل حداقلکننده سعی میکند که کمترین امتیاز ممکن را به دست آورد در حالت معین اگر حداکثرکننده برتری داشته باشد امتیاز مثبت خواهد بود و اگر حداقلکننده برتری داشته باشد امتیاز منفی خواهد بود.
این مقادیر و محاسبه توسط روشهای اکتشافی (پیشبینی حرکتهای ممکن در بازی) که برای هر بازی (منظور نوع بازی است) منحصربهفرد خواهد بود محاسبه میشود.
اوپس، اینطور توضیحدادنش خیلی سخته بگذارید با یک مثال سعی کنم نحوه عملکرد این الگوریتم را بهتر توضیح بدم که در ادامه به آن خواهیم پرداخت.
الگوریتم مینمکس چطور کار میکند
بازیای را در نظر بگیرید که دارای نهایتاً چهار حالت است و مسیرها برای رسیدن به هرکدام از چهار حالت مطابق شکل زیر است.

فرض کنیم شما بازیکن حداکثر کننده هستید و اولین شانس حرکت را دارید، یعنی شما در سطح بالایی هستید و حریف شما در سطح بعدی است. باتوجهبه اینکه حریف شما نیز بهینه بازی میکند، بهعنوان یک حداکثرکننده، کدام حرکت را انتخاب میکنید؟
ازآنجاییکه الگوریتم مینمکس یک الگوریتم بازگشتی است، تمام حالتهای ممکن را چک میکند و بعد از اتمام بررسیها تصمیمگیری میکند ما نیز چنین میکنیم که نحوه عملکرد ملموستر باشد.
- شما به عنوان یک بازیکن حداکثر کننده حرکت L را انتخاب میکنید، آنگاه حریف شما دو انتخاب خواهد داشت یا ۳ را انتخاب کند یا این که ۵ را انتخاب کند که با توجه به نقش حداقلکننده ۳ را انتخاب خواهد کرد.
- شما به عنوان یک بازیکن حداکثر کننده حرکت R را انتخاب میکنید، آنگاه حریف شما دو انتخاب خواهد داشت یا ۲ را انتخاب کند یا این که ۹ را انتخاب کند که با توجه به نقش حداقلکننده مسلما ۲ را انتخاب خواهد کرد.
باتوجهبه شرایط بالا که توضیح دادیم منطقیتر است که شما بهعنوان حداکثرکننده حرکت به سمت چپ (L) را انتخاب کنید که در نهایت در بدترین حالت ممکن ۳ امتیاز خواهید گرفت. در نهایت درخت بازی به شکل زیر تصویر خواهد شد.
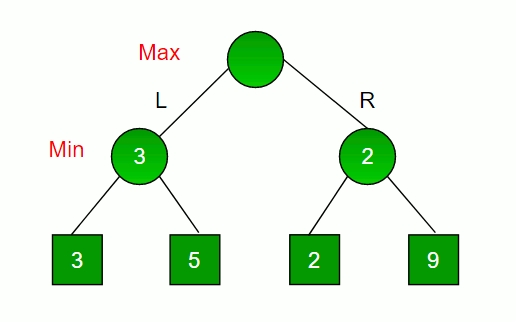
همانطور که در تصویر میبینید اگر به راست بروید در نهایت ۲ امتیاز خواهید گرفت و اگر به چپ بروید ۳ امتیاز خواهید گرفت. در واقع حداقل کننده رقیب شماست که در کل بازی سعی خواهد کرد شما کمترین امتیاز ممکن را کسب کنید و شما مدام در تلاش هستید بیشترین امتیاز را به دست آورید.
منطق شطرنج
در این مقاله به شکل خیلی ساده سعی شد که الگوریتم minmax را با مثال توضیح دهیم چرا که منطق عملکردی هوش شطرنج ما از این الگوریتم استفاده میکند. مثال ذکر شده خیلی ساده بود و فقط هر بازیکن اجازه یک حرکت را داشت که در نهایت ۴ حالت ممکن خواهد بود. در بازیای مثل بازی دوز اولین بازیکن ۹ حالت ممکن خواهد داشت و بازیکن دوم ۸ حالت و همینطور الان آخر …
در بازی شطرنج تعداد حالتهای ممکن قابلشمارش نیست، از طرفی موقعیت هر مهره میتواند در تصمیمگیری تأثیر داشته باشد بااینحال همچنان منطق حاکم پشت انتخاب حرکت همین منطق ساده است.
در مقاله بعد سعی میکنم با استفاده از این الگوریتم و منطق شطرنج یک بازی ساده رو مثل بازی دوز پیادهسازی کنیم که هم درک بهتری از نحوه کار الگوریتم داشته باشید هم نحوه پیادهسازی اونو ببینید
منبع:سیسوگ





