حدود دو سه هفته است بهشدت درگیر الگوریتمهای رمزنگاری شدم، از الگوریتمهای رمزگذاری متقارن تا نامتقارن، واقعاً دنیای پیچیده و جذابی است که بیس اولیه آن ریاضی محض است. قبلاً در مورد اهمیت تولید اعداد تصادفی مقالهای نوشته بودم و به شکل سختافزاری سعی کرده بودم که چالش تولید اعداد تصادفی را حل کنم، اگر کنجکاو هستید بیشتر در مورد آن مطالعه کنید میتوانید مقاله چگونه اعداد تصادفی واقعا تصادفی بسازیم! را مطالعه کنید.
یکی از پایههای مهم تولید کلیدهای رمزگذاری اعداد تصادفی هستند هرچه تولید اعداد تصادفی، تصادفیتر و غیرقابل حدستر باشد، کلید تولیدشده، امنتر خواهد بود. اما تا قبل از آشنایی با کلیدهای نامتقارن به اهمیت وجود اعداد اول پی نبرده بودم.
گهگاه در مقالات دیده بودم که روی بهینهسازی تولید و کشف اعداد اول کار میکردند ولی هیچوقت فکر نکرده بودم چرا تولید این اعداد اینقدر اهمیت دارد و چرا تولید اعداد بزرگ اول در درجه اهمیت بالایی قرار دارد! مثلاً یک عدد اول ۱۲۸ رقمی خوب که چی! بعد از مطالعه ایده RSA که نهایتاً مجبور بودم آن را پیادهسازی کنم چون بهاندازه کافی حافظه در اختیار نداشتم که از کتابخانههای آماده استفاده کنم هرچه بیشتر متوجه اهمیت و زیبایی ریاضیات شدم.
در این مقاله به شکل خیلی ساده و ابتدایی سعی خواهم کرد الگوریتم RSA را توضیح دهم تا با مکانیسم عملکرد آن آشنا شوید. با ما همراه باشید و ما را به دوستان خود معرفی کنید.
وقتی میگوییم رمزگذاری در واقع از چه چیز حرف میزنیم؟
فکر میکنم بهتر باشه مقداری از رمزنگاری حرف بزنیم و کاربردهای آن را در دستگاههای امروزی با هم بررسی کنیم، اول لازمه که بدونیم رمزگذاری اصولا چیز جدیدی نیست، و اولین الگوریتم رمزگذاری شده به ۱۹۰۰ سال قبل از میلاد مسیح برمیگرده، اصولا هدف رمزگذاری ذخیره یا انتقال پیام است به شکلی که تنها افراد مورد اعتماد قادر به درک مفهوم پیام مخابره شده باشند.
در گذشته رمزنگاری بیشتر در جنگها و مراودات حساس حکومتی کاربرد داشته است که فکر میکنم بارزترین نمونه آن را میتوان در جنگ جهانی دوم و دستگاه رمزگذار انیگمای آلمانی دید. آلمانها پیامهای حساس تجاری، نظامی خود را با استفاده از این دستگاه رمزگذاری میکردند که تا مدتها متفقین را برای شکستن رمز آن دچار چالش کرده بود. اگر به تاریخچه جنگ جهانی و رمزنگاری و نحوه شکستن رمز انیگما علاقهمند هستند توصیه میکنم حتما فیلم The Imitation Game را ببینید.
اما امروزه مورد توجه قرار گرفتن حریم خصوصی و تلاش شرکت های تجاری برای رمزگشایی فعالیت شرکتهای رقیب و گسترش روز افزون استفاده از دستگاههای IOT کاربرد رمزگذاری روزانه و در تمام دستگاههای مورد استفاده ما است.
رمزگذاری متقارن و نامتقارن چیست

این روش هرچند کاراست ولی در کاربردهایی دارای معضلات جدیای است. چرا که هر شخصی کلید را داشته باشد قادر به رمز کردن و از رمز خارج کردن پیامها خواهد بود. یعنی برای جلوگیری از شنود و لو رفتن اطلاعات حتماً لازم است که کلید را از روشی منتقل کنید که امن است و مطمئن باشید بههیچعنوان درز نخواهد کرد.
همین مسئله به ظاهر ساده چالشهای زیادی برای شرکتهای بزرگ ایجاد کرد. تا این که الگوریتم رمزگذاری نامتقارن پیشنهاد شد.
در الگوریتم رمزگذاری نامتقارن فرض این است که بستر انتقال اطلاعات ناامن است و هر شخصی اراده کند خواهد توانست هرچه لازم است را شنود کند. پس عملاً نمیتوان از روش متقارن استفاده کرد چون با شنود کلید کل مکالمه قابل رمزگشایی است. برای این مشکل در رمزنگاری نامتقارن به جای یک کلید از دو کلید استفاده شده، که اطلاعات رمز شده با یک کلید، تنها با کلید دیگر قابل رمزگشایی است. به این شکل ما قادر خواهیم بود که کلید اول که کلید Public هم خوانده میشود بدون نگرانی در فضای ناامن منتشر کنیم و کلید خصوصی (کلید دوم) را نزد خود نگه داریم و اطلاعات رمز شده را با استفاده از آن رمزگشایی کنیم که در ادامه به آن خواهیم پرداخت.
مختصری در مورد الگوریتم رمزگذاری RSA
الگوریتمهای زیادی هستند که از کلید نامتقارن استفاده میکنند ولی یکی از اولین آنها که هنوز هم مورداستفاده است و اتفاقاً خیلی محبوب هم هست (البته خیلی محبوب رو مطمئن نیستم ولی بسیار مورد استقبال است) الگوریتم رمزنگاری RSA نخستین روش مورد اعتماد در بین روشهای رمزگذاری دیگر است و البته به جرات میتوان گفت یکی از جهشهای چشمگیر در زمینه رمزگذاری به حساب میآید. امروزه این الگوریتم به شکل گسترده در تقریباً اکثر ارتباطات الکترونیکی مورد استفاده قرار میگیرد.
RSA در واقع از سه حرف اولیه نام مخترعین آن ساخته شده یعنی Ron RIvest, Adi Shamir و Adleman که در سال ۱۹۷۷ این روش را به طور عمومی معرفی کردند.

RSA در واقع الگوریتم کندی است و به همین علت برای تبادل اطلاعات استفاده نمیشود اما به دلیل خاصیت کلید عمومی و خصوصی که میتوان کلید عمومی را بین همه به اشتراک گذاشت بدون این که نگرانی از بابت آن داشت معمولاً برای انتقال کلید یک الگوریتم متقارن استفاده میشود.
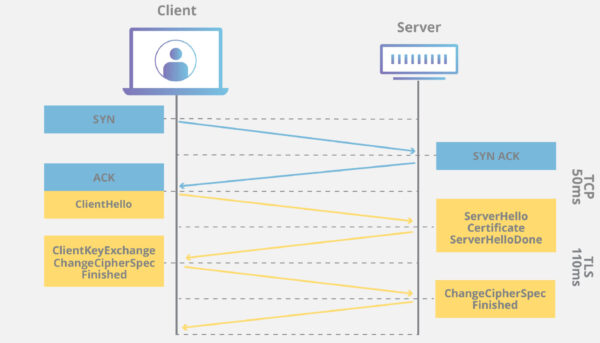
بگذارید یک سناریوی واقعی را برای روشن شدن عملکرد آن مثال بزنیم، برای باز کردن یک وب سایت که به شکل https است، ابتدا مرورگر شما درخواستی را به سرور ارسال میکند، سرور در پاسخ کلیدهای عمومی RSA را برای مرورگر شما ارسال میکند، بعد از تأیید مرورگر سرور کلید یکی از الگوریتمهای رمزنگاری متقارن را که مورد پذیرش مرورگر شماست را با استفاده از RSA به مرورگر شما ارسال میکند (مثلاً کلید AES256) پس از آن تمام ارتباطهای بین مرورگر شما و سرور براساس روش متقارن AES صورت خواهد گرفت.
اما الگوریتم رمزگذاری RSA چطور این کار رو انجام میدهد
از آنجایی که قرار نیست وارد اثبات ریاضی تئوری RSA بشم هرچند که اثباتش هم به اندازه کافی جذاب هست، سعی میکنم که نحوه کارکردش را به شکل خیلی ساده و با استفاده از یک مثال توضیح بدیم. برای همین نیاز به یک سناریو داریم که آن را اینطور تعریف میکنیم:
فرض کنید مرورگر شما قصد دارد عدد ۱۴ (که آن را با برچسب P نمایش میدهم) را بعد از رمزنگاری به سرور ارسال کند،سرور بعد از دریافت عبارت رمزنگاری شده آن را رمزگشایی کند و به مقدار اصلی برگرداند. در این مثال ما از اعداد کوچک استفاده میکنیم برای آنکه شما قادر باشید به شکل ذهنی یا بر روی کاغذ اتفاق های رخ داده را دنبال کنید. در ادامه گام هایی که برای این تراکنش طی میشود را به شکل اجمالی بررسی میکنیم :
قبل از هرگونه ارتباطی سرور باید کلید های عمومی و خصوصی را ایجاد کند.
- برای شروع تراکنش مرورگر باید از سرور کلید عمومی را دریافت کند، این کار معمولا با درخواستی از سمت مرورگر انجام میشود.
- در پاسخ سرور کلید های عمومی را که شامل k=7 و n=33 است را به مرورگر تحویل میدهد.
- مرورگر با استفاده از کلید دریافت شده متن خود (P=14) را رمز میکند و عبارت رمز شده E=20 را به سرور ارسال میکند.
- سرور پیام رمز شده E=20 را دریافت میکند و با استفاده از کلید خصوصی خود J=3 و البته کلید عمومی n=33 پیام رمز شده E=20 را به پیام اصلی یعنی P=14 رمزگشایی میکند.
حالا که با روند کلی ارتباط الگوریتم RSA آشنا شدیم با جزییات بیشتری مراحل را بررسی میکنیم:
مرحله اول: ساخت کلید عمومی و خصوصی توسط سرور
۱. به شکل کاملاً تصادفی دو عدد اول (prime number) هرچه بزرگتر بهتر را انتخاب میکنیم. فرض کنید ما دو عدد p=3 و q=11 را انتخاب کردیم.
۲. با استفاده از این دو عدد n جزء کلید عمومی را محاسبه میکنیم به شکل زیر (که با توجه به مقادیر انتخاب شده مقدار ۳۳ خواهد داشت)
n = p * q = 3 * 11 = 33
z = ( p - 1 ) * ( q - 1 ) => ( 3 - 1 ) * ( 11 - 1 ) = 20
۴. حالا عدد اول k را باید به نحوی انتخاب کنیم که نسبت به z هم اول باشد، یعنی z بر k بخشپذیر نباشد. برای مثال ما میتوانیم مقادیر ۷، ۱۱، ۱۳، ۱۷ یا ۱۹ را انتخاب کنیم اما از ۵ نمیتوانیم استفاده کنیم زیرا ۲۰ بر ۵ بخش پذیر است. بیایید کوچکترین عدد را انتخاب کنیم یعنی k=7. (البته هرچه عدد بزرگتر باشه بهتر است اما چون قرار ذهنی محاسبات رو جلو ببریم عدد کوچکتر یعنی محاسبه کمتر:))
۵. خوب تا اینجا ما کلید عمومی را ساختیم یعنی n=33 و k=7
۶. قبل از شروع هر تراکنشی باید کلید خصوصی را نیز ایجاد کنیم که طبق فرمول زیر عمل میکنیم
(k * j) % z= 1
مقدار j که درواقع همان کلید خصوصی ما است با استفاده از این رابطه محاسبه میشود. ما باید عددی به عنوان j انتخاب کنیم که علاوه بر این که اول باشد، حاصل ضرب آن در k و باقیمانده آن بر z عدد یک شود. در این مثال می توانیم j=3 را انتخاب کنیم.
(7 * j) % 20 = 1 -> j=3 => (7 * 3) % 20 = 1
خوب تا اینجا کلید عمومی (k=7 , n=33) و خصوصی (j=3) را محاسبه کردیم. دقت داشته باشد به هیچ وجه کلید خصوصی را نباید در اختیار کاربر قرار دهید.
مرحله دوم: رمزنگاری پیام در مرورگر
برای رمزنگاری پیام تنها کافی است از رابطه زیر استفاده کنیم، در سناریوی تعریف شده قرار بود که ما مقدار P=14 را رمز کنیم و به سرور ارسال کنیم.
(P ^ k) % n = E
در فرمول بالا منظور «^» توان است
و منظور از n و k کلیدهای عمومی هستند که از سرور دریافت شده اند
و منظور از P پیامی است که قرار است رمز شود
و E متن رمز شده است که نتیجه فرمول بالاست
(14 ^ 7) % 33 = 20
با جایگذاری اعداد محاسبه شده، در نهایت ما E=20 را خواهیم داشت که آن را به سرور ارسال میکنیم.
مرحله سوم: رمزگشایی پیام در سرور
در این مرحله سرور پیام رمز شده از کلایت را دریافت میکند و بعد از آن با استفاده از فرمول زیر از پیام رمز شده به پیام اصلی می رسد.
(E ^ j) % n = P
- در فرمول بالا منظور «^» توان است
- و منظور از j کلید خصوصی است
- n نیز بخشی از کلید عمومی است که قبلا محاسبه شده
- E پیام رمز شده است
- P پیامی است که کاربر ارسال کرده است
- با جایگذاری اعداد متناسب در فرمول بالا عدد رمز نشده نمایان خواهد شد.
(20 ^ 3) % 33 = 14
به همین سادگی و خوشمزگی ? ما در این مقاله در مورد تئوری های پشت فرمول صحبت نکردیم، صرفا سعی کردیم خیلی ساده عملکرد آن را نشان دهیم، امیدوارم که حداقل تصوری در خصوص عملکرد این الگوریتم رمزنگاری پیدا کرده باشید.
آیا شکستن کد الگوریتم RSA ممکن است
شرط اساسی الگوریتم رمزگذاری RSA این است که کلیدهای عمومی و خصوصی از نظر ریاضی به هم وابسته هستند، اما تعیین این رابطه باید از نظر فرد خارجی بسیار سخت باشد تا امنیت ارتباط حفظ شود. همانطور که در ابتدای مقاله (ساخت کلید) دیدید همه چیز از اعداد p و q شروع میشود که ما n را با استفاده از آنها محاسبه کردیم.
کلید عمومی از دو عدد n و k درست شده است که k از z و z از p و q درست شدهاند، کلید خصوصی j با استفاده از k و z محاسبه میشود و همانطور که گفتیم k و z هم از p و q محاسبه شدهاند. بنابر این j میتواند از p و q نیز محاسبه شود که ثابت میکند کلیدهای عمومی و خصوصی از نظر ریاضی به هم وابسته هستند.
بنابراین اگر یک فرد خارجی بخواهد کلید خصوصی j را محاسبه کند، نیاز است که n را به دو عدد اولی که از آن ساخته شدهاند تجزیه کند، به نوعی میتوان گفت پاشنه آشیل الگوریتم همینجاست، اگر n عدد بسیار بزرگی باشد تقریباً پیدا تجزیه آن به دو عدد اول سازنده کار غیرممکنی است. برای همین است که در محاسبه کلیدها از اعداد بسیار بزرگ استفاده میشود.
اعدادی که برای ذخیره سازی آنها نیاز به ۱۰۲۴ یا ۲۰۴۸ و حتی ۴۰۹۶ بیت حافظه است. تصور عددی که ۲۰۴۸ بیت برای ذخیره سازی آن لازم است چقدر بزرگ خواهد بود و به همان نسبت تجزیه آن چقدر کار دشواری است و چه توان پردازشی لازم است.
یکی از دلایل کندی الگوریتم رمزنگاری RSA استفاده از این اعداد بزرگ است که کامپیوتر باید عملیات ریاضی توان و باقی مانده را بر روی اعدادی این چنین بزرگ انجام دهد و به نظر من سختی فزاینده وقتی است که قصد داشته باشیم اعداد اول این چنین بزرگ برای p و q پیدا کنیم.
منبع:سیسوگ





